Bayesian interpretation of SGD as Ito process
Paper and Code
Nov 20, 2019
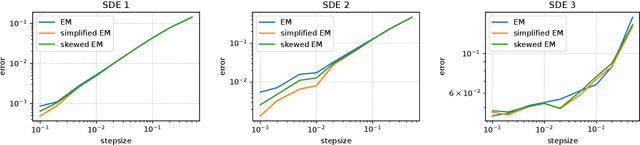
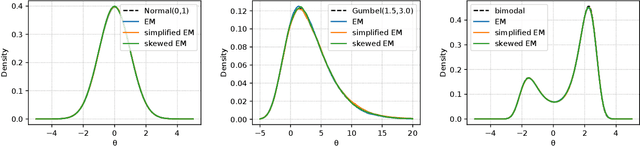

The current interpretation of stochastic gradient descent (SGD) as a stochastic process lacks generality in that its numerical scheme restricts continuous-time dynamics as well as the loss function and the distribution of gradient noise. We introduce a simplified scheme with milder conditions that flexibly interprets SGD as a discrete-time approximation of an Ito process. The scheme also works as a common foundation of SGD and stochastic gradient Langevin dynamics (SGLD), providing insights into their asymptotic properties. We investigate the convergence of SGD with biased gradient in terms of the equilibrium mode and the overestimation problem of the second moment of SGLD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge