Poisson-Dirac Neural Networks for Modeling Coupled Dynamical Systems across Domains

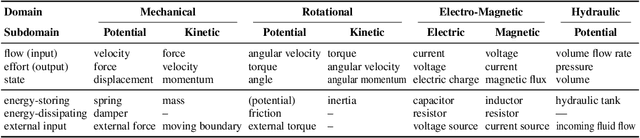
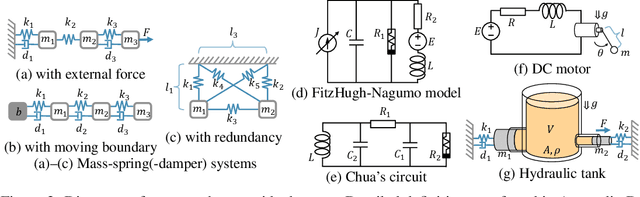
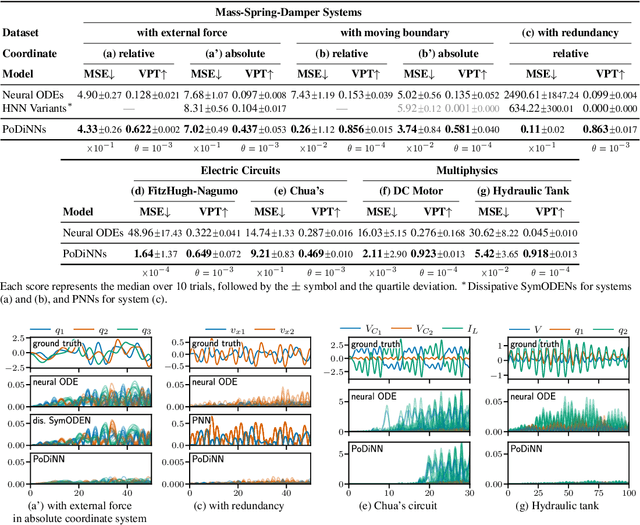
Deep learning has achieved great success in modeling dynamical systems, providing data-driven simulators to predict complex phenomena, even without known governing equations. However, existing models have two major limitations: their narrow focus on mechanical systems and their tendency to treat systems as monolithic. These limitations reduce their applicability to dynamical systems in other domains, such as electrical and hydraulic systems, and to coupled systems. To address these limitations, we propose Poisson-Dirac Neural Networks (PoDiNNs), a novel framework based on the Dirac structure that unifies the port-Hamiltonian and Poisson formulations from geometric mechanics. This framework enables a unified representation of various dynamical systems across multiple domains as well as their interactions and degeneracies arising from couplings. Our experiments demonstrate that PoDiNNs offer improved accuracy and interpretability in modeling unknown coupled dynamical systems from data.

Neural Operators Meet Energy-based Theory: Operator Learning for Hamiltonian and Dissipative PDEs

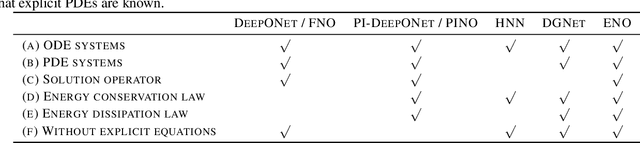
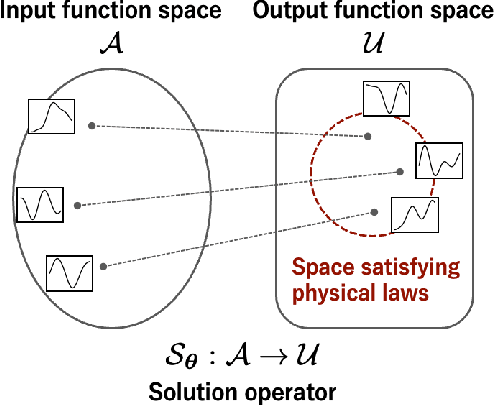
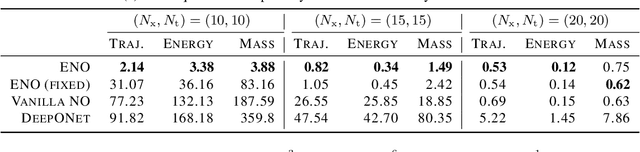
The operator learning has received significant attention in recent years, with the aim of learning a mapping between function spaces. Prior works have proposed deep neural networks (DNNs) for learning such a mapping, enabling the learning of solution operators of partial differential equations (PDEs). However, these works still struggle to learn dynamics that obeys the laws of physics. This paper proposes Energy-consistent Neural Operators (ENOs), a general framework for learning solution operators of PDEs that follows the energy conservation or dissipation law from observed solution trajectories. We introduce a novel penalty function inspired by the energy-based theory of physics for training, in which the energy functional is modeled by another DNN, allowing one to bias the outputs of the DNN-based solution operators to ensure energetic consistency without explicit PDEs. Experiments on multiple physical systems show that ENO outperforms existing DNN models in predicting solutions from data, especially in super-resolution settings.

Good Lattice Training: Physics-Informed Neural Networks Accelerated by Number Theory

Physics-informed neural networks (PINNs) offer a novel and efficient approach to solving partial differential equations (PDEs). Their success lies in the physics-informed loss, which trains a neural network to satisfy a given PDE at specific points and to approximate the solution. However, the solutions to PDEs are inherently infinite-dimensional, and the distance between the output and the solution is defined by an integral over the domain. Therefore, the physics-informed loss only provides a finite approximation, and selecting appropriate collocation points becomes crucial to suppress the discretization errors, although this aspect has often been overlooked. In this paper, we propose a new technique called good lattice training (GLT) for PINNs, inspired by number theoretic methods for numerical analysis. GLT offers a set of collocation points that are effective even with a small number of points and for multi-dimensional spaces. Our experiments demonstrate that GLT requires 2--20 times fewer collocation points (resulting in lower computational cost) than uniformly random sampling or Latin hypercube sampling, while achieving competitive performance.

FINDE: Neural Differential Equations for Finding and Preserving Invariant Quantities

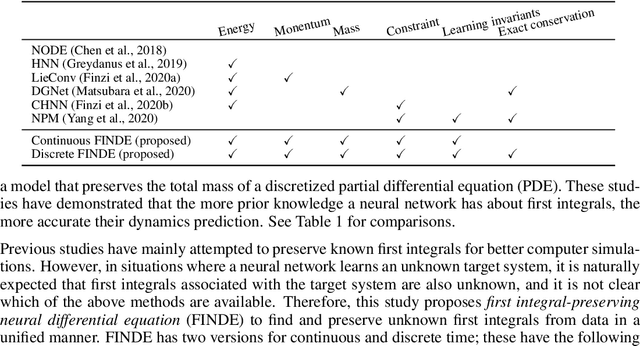
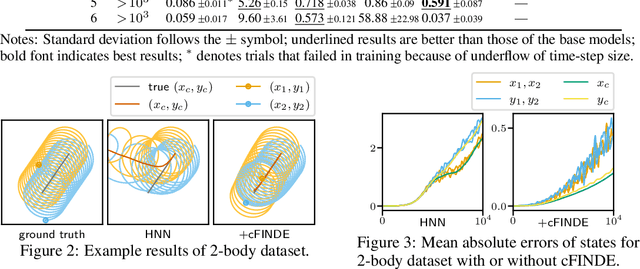
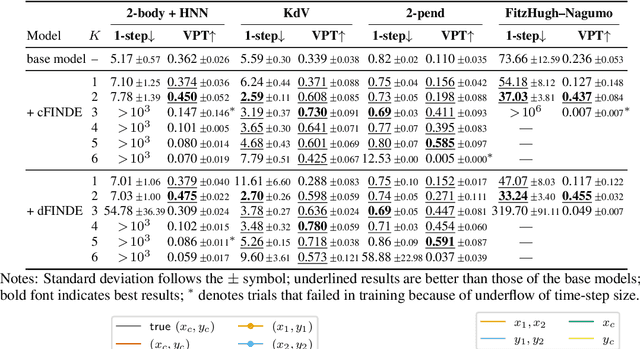
Many real-world dynamical systems are associated with first integrals (a.k.a. invariant quantities), which are quantities that remain unchanged over time. The discovery and understanding of first integrals are fundamental and important topics both in the natural sciences and in industrial applications. First integrals arise from the conservation laws of system energy, momentum, and mass, and from constraints on states; these are typically related to specific geometric structures of the governing equations. Existing neural networks designed to ensure such first integrals have shown excellent accuracy in modeling from data. However, these models incorporate the underlying structures, and in most situations where neural networks learn unknown systems, these structures are also unknown. This limitation needs to be overcome for scientific discovery and modeling of unknown systems. To this end, we propose first integral-preserving neural differential equation (FINDE). By leveraging the projection method and the discrete gradient method, FINDE finds and preserves first integrals from data, even in the absence of prior knowledge about underlying structures. Experimental results demonstrate that FINDE can predict future states of target systems much longer and find various quantities consistent with well-known first integrals in a unified manner.

Universal Approximation Properties of Neural Networks for Energy-Based Physical Systems

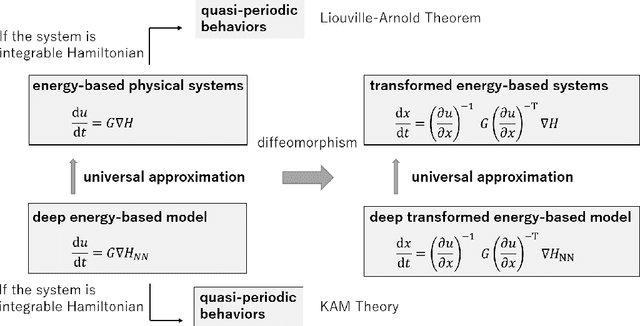
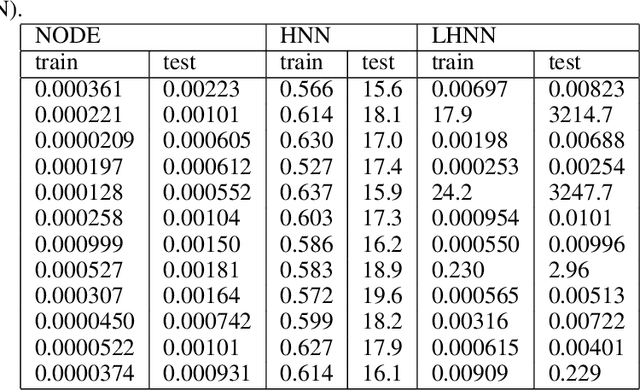
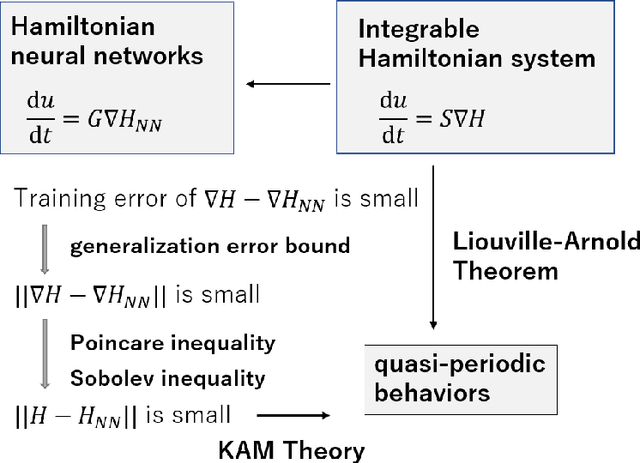
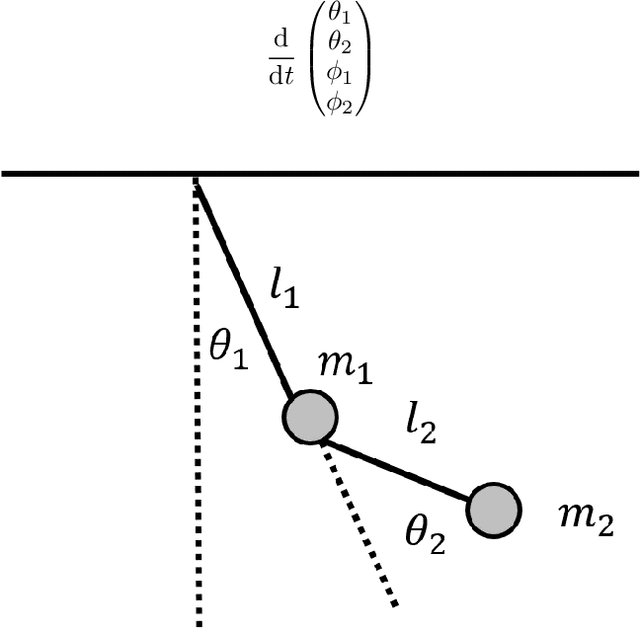
In Hamiltonian mechanics and the Landau theory, many physical phenomena are modeled using energy. In this paper, we prove the universal approximation property of neural network models for such physical phenomena. We also discuss behaviors of the models for integrable Hamiltonian systems when the loss function does not vanish completely by applying the KAM theory.

Symplectic Adjoint Method for Exact Gradient of Neural ODE with Minimal Memory

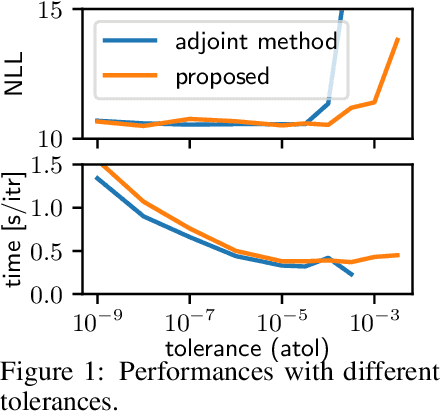
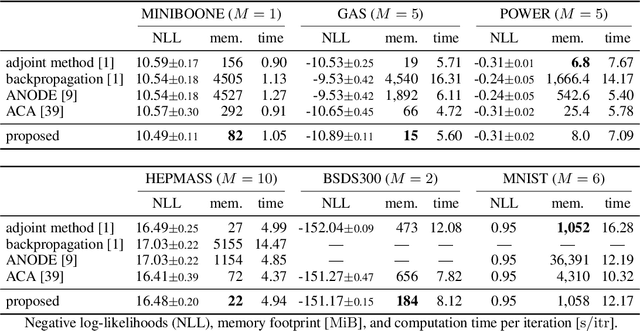
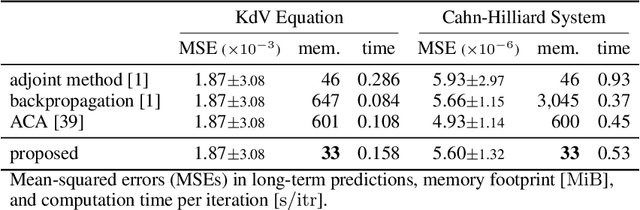
A neural network model of a differential equation, namely neural ODE, has enabled us to learn continuous-time dynamical systems and probabilistic distributions with a high accuracy. It uses the same network repeatedly during a numerical integration. Hence, the backpropagation algorithm requires a memory footprint proportional to the number of uses times the network size. This is true even if a checkpointing scheme divides the computational graph into sub-graphs. Otherwise, the adjoint method obtains a gradient by a numerical integration backward in time with a minimal memory footprint; however, it suffers from numerical errors. This study proposes the symplectic adjoint method, which obtains the exact gradient (up to rounding error) with a footprint proportional to the number of uses plus the network size. The experimental results demonstrate the symplectic adjoint method occupies the smallest footprint in most cases, functions faster in some cases, and is robust to a rounding error among competitive methods.

Automatic discrete differentiation and its applications

In this paper, a method for automatically deriving energy-preserving numerical methods for the Euler-Lagrange equation and the Hamilton equation is proposed. The derived energy-preserving scheme is based on the discrete gradient method. In the proposed approach, the discrete gradient, which is a key tool for designing the scheme, is automatically computed by a similar algorithm to the automatic differentiation. Besides, the discrete gradient coincides with the usual gradient if the two arguments required to define the discrete gradient are the same. Hence the proposed method is an extension of the automatic differentiation in the sense that the proposed method derives not only the discrete gradient but also the usual gradient. Due to this feature, both energy-preserving integrators and variational (and hence symplectic) integrators can be implemented in the same programming code simultaneously. This allows users to freely switch between the energy-preserving numerical method and the symplectic numerical method in accordance with the problem-setting and other requirements. As applications, an energy-preserving numerical scheme for a nonlinear wave equation and a training algorithm of artificial neural networks derived from an energy-dissipative numerical scheme are shown.