Structure-Preserving Physics-Informed Neural Networks With Energy or Lyapunov Structure

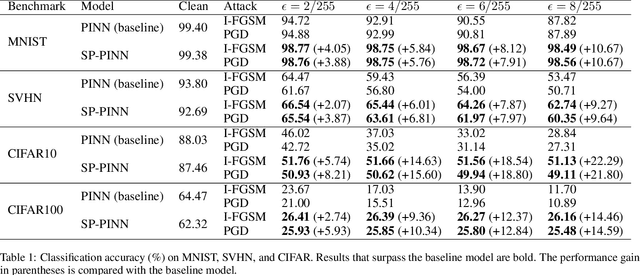
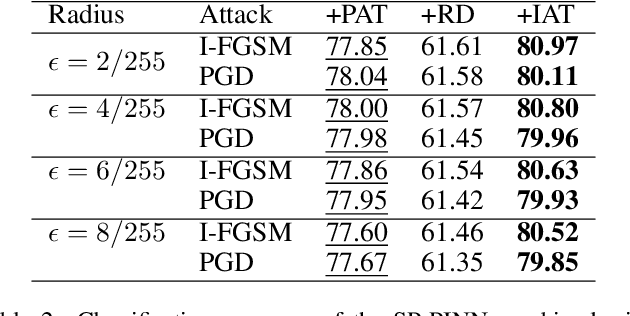
Recently, there has been growing interest in using physics-informed neural networks (PINNs) to solve differential equations. However, the preservation of structure, such as energy and stability, in a suitable manner has yet to be established. This limitation could be a potential reason why the learning process for PINNs is not always efficient and the numerical results may suggest nonphysical behavior. Besides, there is little research on their applications on downstream tasks. To address these issues, we propose structure-preserving PINNs to improve their performance and broaden their applications for downstream tasks. Firstly, by leveraging prior knowledge about the physical system, a structure-preserving loss function is designed to assist the PINN in learning the underlying structure. Secondly, a framework that utilizes structure-preserving PINN for robust image recognition is proposed. Here, preserving the Lyapunov structure of the underlying system ensures the stability of the system. Experimental results demonstrate that the proposed method improves the numerical accuracy of PINNs for partial differential equations. Furthermore, the robustness of the model against adversarial perturbations in image data is enhanced.

A modified model for topic detection from a corpus and a new metric evaluating the understandability of topics

This paper presents a modified neural model for topic detection from a corpus and proposes a new metric to evaluate the detected topics. The new model builds upon the embedded topic model incorporating some modifications such as document clustering. Numerical experiments suggest that the new model performs favourably regardless of the document's length. The new metric, which can be computed more efficiently than widely-used metrics such as topic coherence, provides variable information regarding the understandability of the detected topics.

Composing a surrogate observation operator for sequential data assimilation

In data assimilation, state estimation is not straightforward when the observation operator is unknown. This study proposes a method for composing a surrogate operator for a true operator. The surrogate model is improved iteratively to decrease the difference between the observations and the results of the surrogate model, and a neural network is adopted in the process. A twin experiment suggests that the proposed method outperforms approaches that use a specific operator that is given tentatively throughout the data assimilation process.

Symplectic Adjoint Method for Exact Gradient of Neural ODE with Minimal Memory

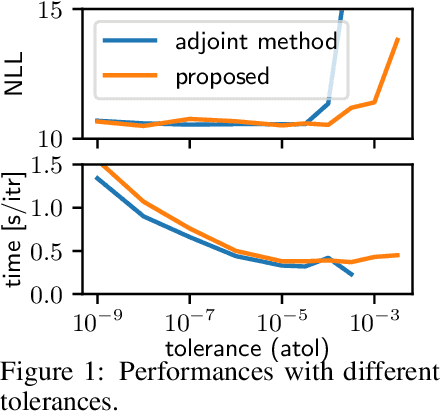
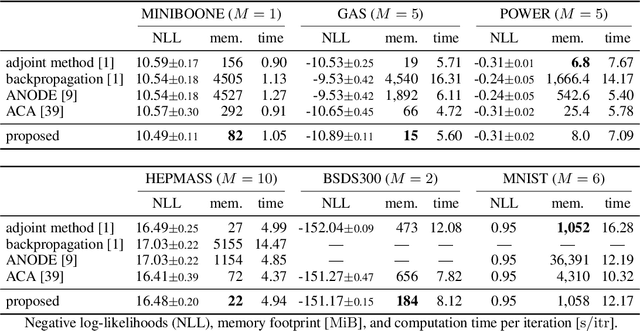
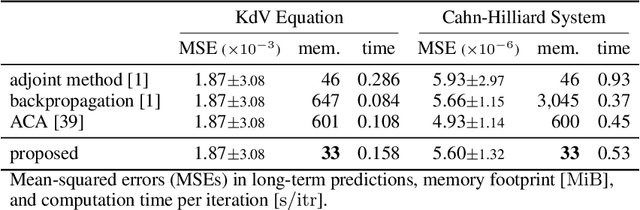
A neural network model of a differential equation, namely neural ODE, has enabled us to learn continuous-time dynamical systems and probabilistic distributions with a high accuracy. It uses the same network repeatedly during a numerical integration. Hence, the backpropagation algorithm requires a memory footprint proportional to the number of uses times the network size. This is true even if a checkpointing scheme divides the computational graph into sub-graphs. Otherwise, the adjoint method obtains a gradient by a numerical integration backward in time with a minimal memory footprint; however, it suffers from numerical errors. This study proposes the symplectic adjoint method, which obtains the exact gradient (up to rounding error) with a footprint proportional to the number of uses plus the network size. The experimental results demonstrate the symplectic adjoint method occupies the smallest footprint in most cases, functions faster in some cases, and is robust to a rounding error among competitive methods.