Poisson-Dirac Neural Networks for Modeling Coupled Dynamical Systems across Domains

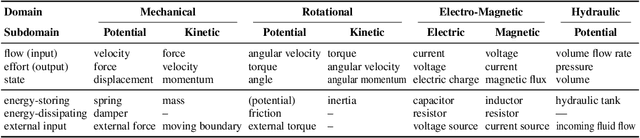
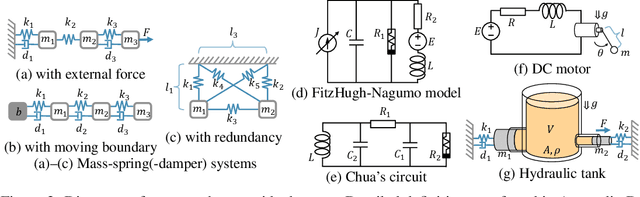
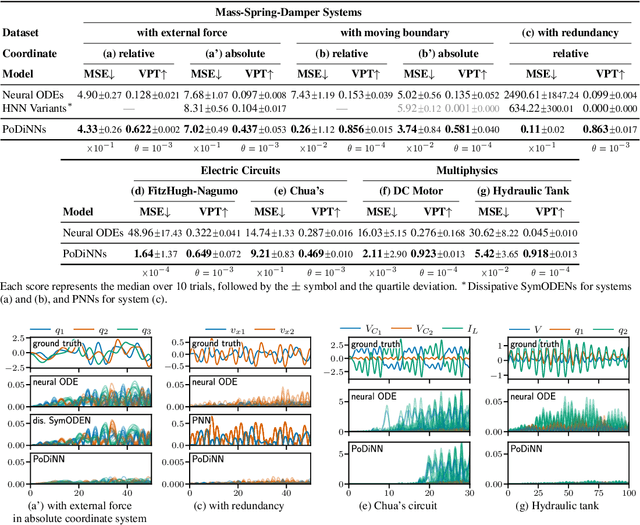
Deep learning has achieved great success in modeling dynamical systems, providing data-driven simulators to predict complex phenomena, even without known governing equations. However, existing models have two major limitations: their narrow focus on mechanical systems and their tendency to treat systems as monolithic. These limitations reduce their applicability to dynamical systems in other domains, such as electrical and hydraulic systems, and to coupled systems. To address these limitations, we propose Poisson-Dirac Neural Networks (PoDiNNs), a novel framework based on the Dirac structure that unifies the port-Hamiltonian and Poisson formulations from geometric mechanics. This framework enables a unified representation of various dynamical systems across multiple domains as well as their interactions and degeneracies arising from couplings. Our experiments demonstrate that PoDiNNs offer improved accuracy and interpretability in modeling unknown coupled dynamical systems from data.

Good Lattice Training: Physics-Informed Neural Networks Accelerated by Number Theory

Physics-informed neural networks (PINNs) offer a novel and efficient approach to solving partial differential equations (PDEs). Their success lies in the physics-informed loss, which trains a neural network to satisfy a given PDE at specific points and to approximate the solution. However, the solutions to PDEs are inherently infinite-dimensional, and the distance between the output and the solution is defined by an integral over the domain. Therefore, the physics-informed loss only provides a finite approximation, and selecting appropriate collocation points becomes crucial to suppress the discretization errors, although this aspect has often been overlooked. In this paper, we propose a new technique called good lattice training (GLT) for PINNs, inspired by number theoretic methods for numerical analysis. GLT offers a set of collocation points that are effective even with a small number of points and for multi-dimensional spaces. Our experiments demonstrate that GLT requires 2--20 times fewer collocation points (resulting in lower computational cost) than uniformly random sampling or Latin hypercube sampling, while achieving competitive performance.

Deep Curvilinear Editing: Commutative and Nonlinear Image Manipulation for Pretrained Deep Generative Model

Semantic editing of images is the fundamental goal of computer vision. Although deep learning methods, such as generative adversarial networks (GANs), are capable of producing high-quality images, they often do not have an inherent way of editing generated images semantically. Recent studies have investigated a way of manipulating the latent variable to determine the images to be generated. However, methods that assume linear semantic arithmetic have certain limitations in terms of the quality of image editing, whereas methods that discover nonlinear semantic pathways provide non-commutative editing, which is inconsistent when applied in different orders. This study proposes a novel method called deep curvilinear editing (DeCurvEd) to determine semantic commuting vector fields on the latent space. We theoretically demonstrate that owing to commutativity, the editing of multiple attributes depends only on the quantities and not on the order. Furthermore, we experimentally demonstrate that compared to previous methods, the nonlinear and commutative nature of DeCurvEd facilitates the disentanglement of image attributes and provides higher-quality editing.

FINDE: Neural Differential Equations for Finding and Preserving Invariant Quantities

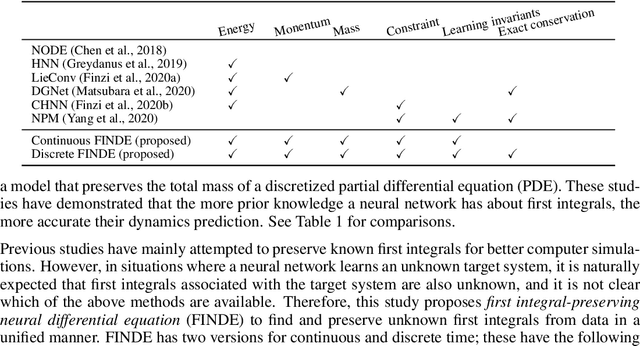
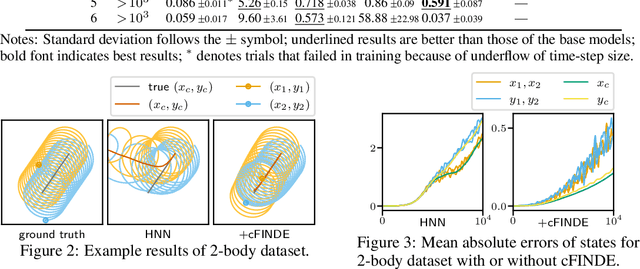
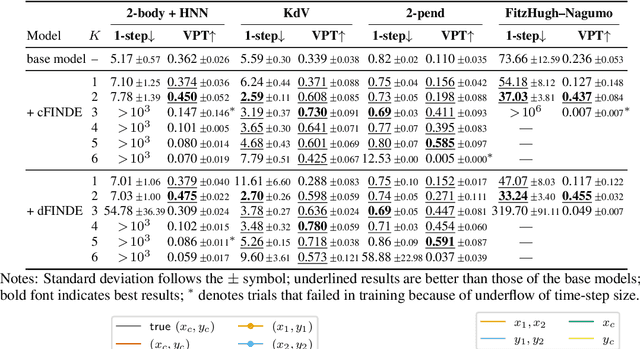
Many real-world dynamical systems are associated with first integrals (a.k.a. invariant quantities), which are quantities that remain unchanged over time. The discovery and understanding of first integrals are fundamental and important topics both in the natural sciences and in industrial applications. First integrals arise from the conservation laws of system energy, momentum, and mass, and from constraints on states; these are typically related to specific geometric structures of the governing equations. Existing neural networks designed to ensure such first integrals have shown excellent accuracy in modeling from data. However, these models incorporate the underlying structures, and in most situations where neural networks learn unknown systems, these structures are also unknown. This limitation needs to be overcome for scientific discovery and modeling of unknown systems. To this end, we propose first integral-preserving neural differential equation (FINDE). By leveraging the projection method and the discrete gradient method, FINDE finds and preserves first integrals from data, even in the absence of prior knowledge about underlying structures. Experimental results demonstrate that FINDE can predict future states of target systems much longer and find various quantities consistent with well-known first integrals in a unified manner.

Cancer Subtyping by Improved Transcriptomic Features Using Vector Quantized Variational Autoencoder

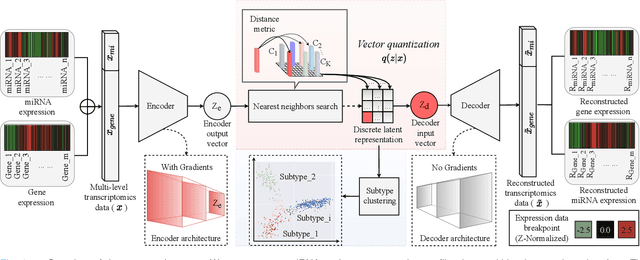
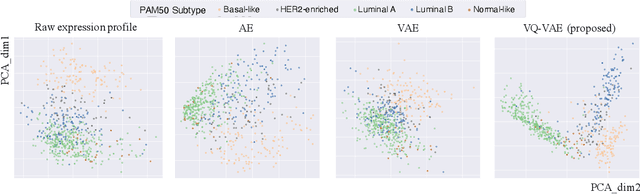
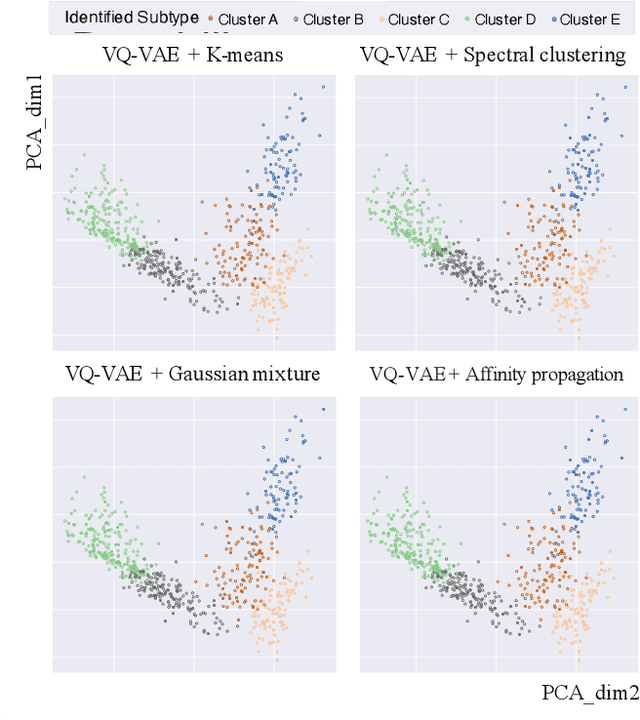
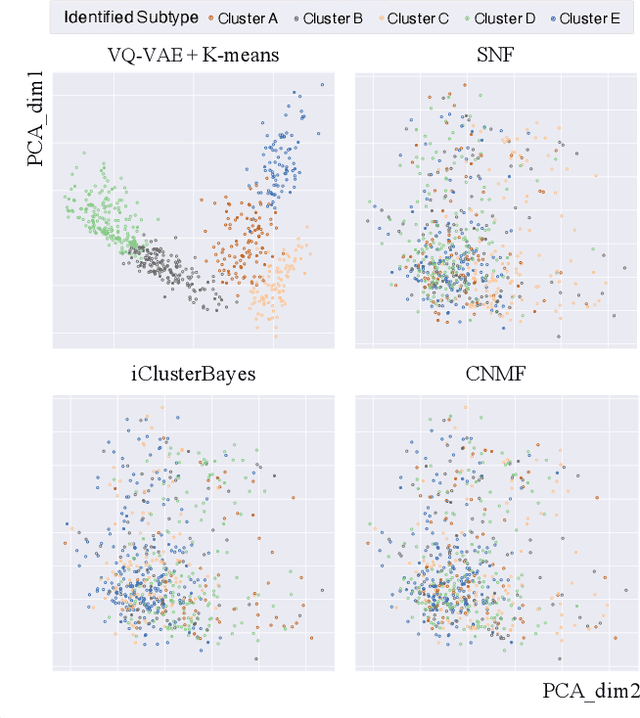
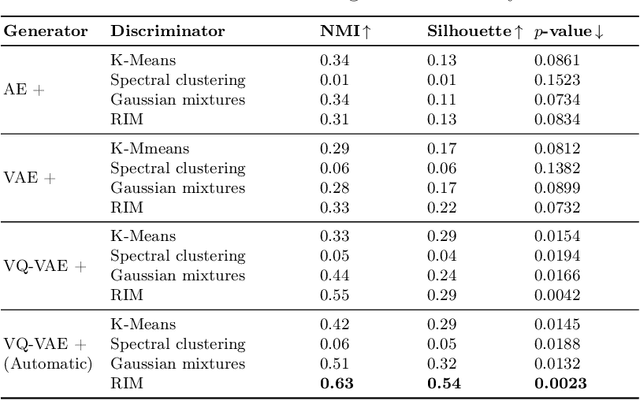
Defining and separating cancer subtypes is essential for facilitating personalized therapy modality and prognosis of patients. The definition of subtypes has been constantly recalibrated as a result of our deepened understanding. During this recalibration, researchers often rely on clustering of cancer data to provide an intuitive visual reference that could reveal the intrinsic characteristics of subtypes. The data being clustered are often omics data such as transcriptomics that have strong correlations to the underlying biological mechanism. However, while existing studies have shown promising results, they suffer from issues associated with omics data: sample scarcity and high dimensionality. As such, existing methods often impose unrealistic assumptions to extract useful features from the data while avoiding overfitting to spurious correlations. In this paper, we propose to leverage a recent strong generative model, Vector Quantized Variational AutoEncoder (VQ-VAE), to tackle the data issues and extract informative latent features that are crucial to the quality of subsequent clustering by retaining only information relevant to reconstructing the input. VQ-VAE does not impose strict assumptions and hence its latent features are better representations of the input, capable of yielding superior clustering performance with any mainstream clustering method. Extensive experiments and medical analysis on multiple datasets comprising 10 distinct cancers demonstrate the VQ-VAE clustering results can significantly and robustly improve prognosis over prevalent subtyping systems.

Automated Cancer Subtyping via Vector Quantization Mutual Information Maximization

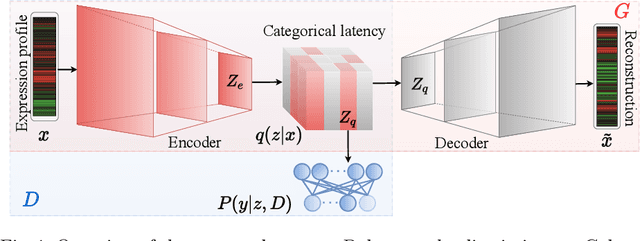
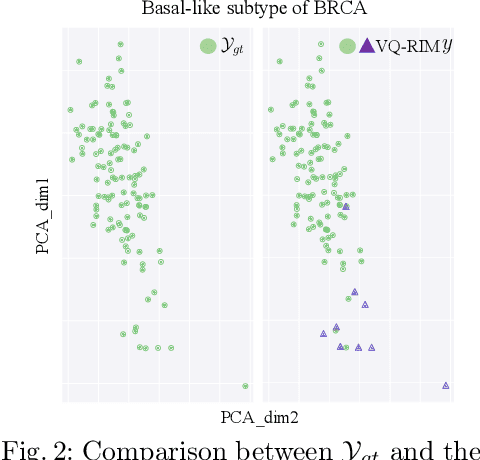
Cancer subtyping is crucial for understanding the nature of tumors and providing suitable therapy. However, existing labelling methods are medically controversial, and have driven the process of subtyping away from teaching signals. Moreover, cancer genetic expression profiles are high-dimensional, scarce, and have complicated dependence, thereby posing a serious challenge to existing subtyping models for outputting sensible clustering. In this study, we propose a novel clustering method for exploiting genetic expression profiles and distinguishing subtypes in an unsupervised manner. The proposed method adaptively learns categorical correspondence from latent representations of expression profiles to the subtypes output by the model. By maximizing the problem -- agnostic mutual information between input expression profiles and output subtypes, our method can automatically decide a suitable number of subtypes. Through experiments, we demonstrate that our proposed method can refine existing controversial labels, and, by further medical analysis, this refinement is proven to have a high correlation with cancer survival rates.

Universal Approximation Properties of Neural Networks for Energy-Based Physical Systems

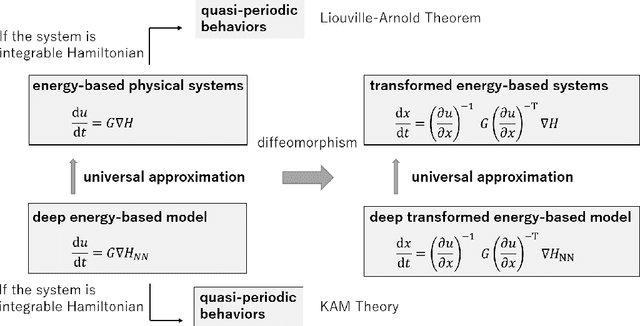
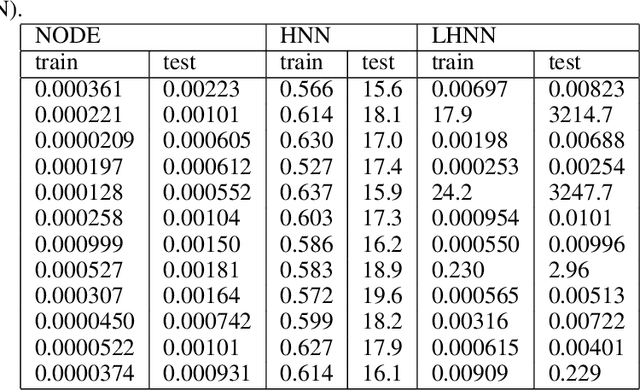
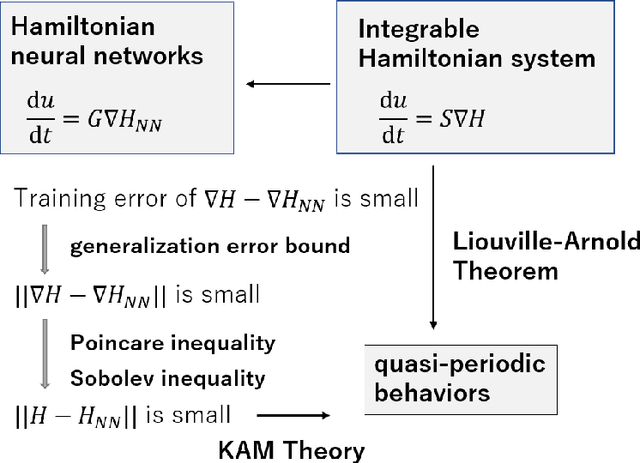
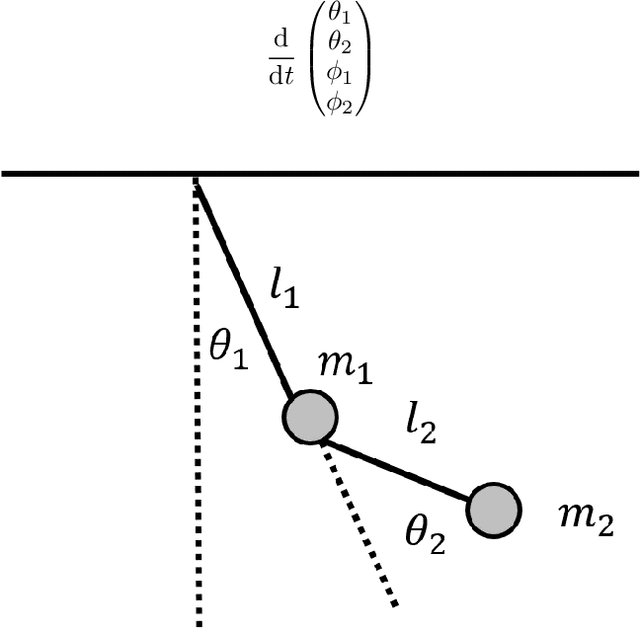
In Hamiltonian mechanics and the Landau theory, many physical phenomena are modeled using energy. In this paper, we prove the universal approximation property of neural network models for such physical phenomena. We also discuss behaviors of the models for integrable Hamiltonian systems when the loss function does not vanish completely by applying the KAM theory.

Symplectic Adjoint Method for Exact Gradient of Neural ODE with Minimal Memory

A neural network model of a differential equation, namely neural ODE, has enabled us to learn continuous-time dynamical systems and probabilistic distributions with a high accuracy. It uses the same network repeatedly during a numerical integration. Hence, the backpropagation algorithm requires a memory footprint proportional to the number of uses times the network size. This is true even if a checkpointing scheme divides the computational graph into sub-graphs. Otherwise, the adjoint method obtains a gradient by a numerical integration backward in time with a minimal memory footprint; however, it suffers from numerical errors. This study proposes the symplectic adjoint method, which obtains the exact gradient (up to rounding error) with a footprint proportional to the number of uses plus the network size. The experimental results demonstrate the symplectic adjoint method occupies the smallest footprint in most cases, functions faster in some cases, and is robust to a rounding error among competitive methods.

ChartPointFlow for Topology-Aware 3D Point Cloud Generation

A point cloud serves as a representation of the surface of a three-dimensional shape. Deep generative models have been adapted to model their variations typically by a map from a ball-like set of latent variables. However, previous approaches have not paid much attention to the topological structure of a point cloud; a continuous map cannot express the varying number of holes and intersections. Moreover, a point cloud is often composed of multiple subparts, and it is also hardly expressed. In this paper, we propose ChartPointFlow, which is a flow-based generative model with multiple latent labels. By maximizing the mutual information, a map conditioned by a label is assigned to a continuous subset of a given point cloud, like a chart of a manifold. This enables our proposed model to preserve the topological structure with clear boundaries, while previous approaches tend to suffer from blurs and to fail in generating holes. Experimental results demonstrate that ChartPointFlow achieves the state-of-the-art performance in generation and reconstruction among sampling-based point cloud generators.

Target-Oriented Deformation of Visual-Semantic Embedding Space

Multimodal embedding is a crucial research topic for cross-modal understanding, data mining, and translation. Many studies have attempted to extract representations from given entities and align them in a shared embedding space. However, because entities in different modalities exhibit different abstraction levels and modality-specific information, it is insufficient to embed related entities close to each other. In this study, we propose the Target-Oriented Deformation Network (TOD-Net), a novel module that continuously deforms the embedding space into a new space under a given condition, thereby adjusting similarities between entities. Unlike methods based on cross-modal attention, TOD-Net is a post-process applied to the embedding space learned by existing embedding systems and improves their performances of retrieval. In particular, when combined with cutting-edge models, TOD-Net gains the state-of-the-art cross-modal retrieval model associated with the MSCOCO dataset. Qualitative analysis reveals that TOD-Net successfully emphasizes entity-specific concepts and retrieves diverse targets via handling higher levels of diversity than existing models.