Symplectic Adjoint Method for Exact Gradient of Neural ODE with Minimal Memory
Paper and Code
Feb 19, 2021
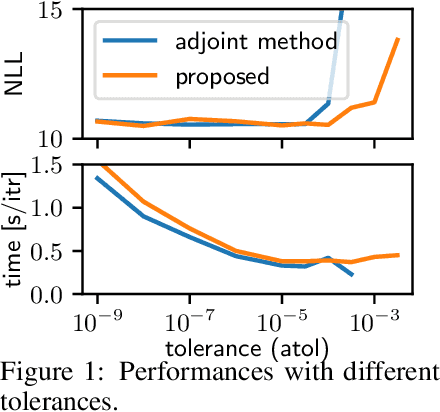
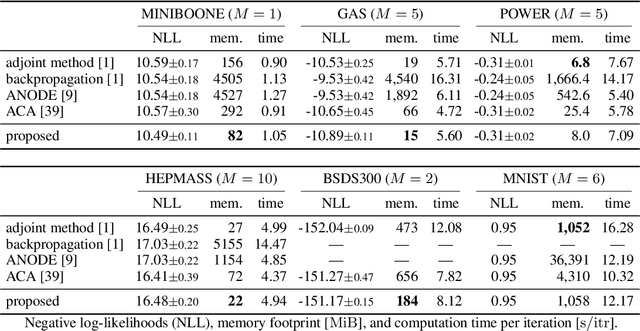
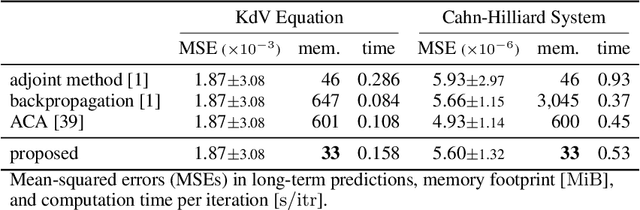
A neural network model of a differential equation, namely neural ODE, has enabled us to learn continuous-time dynamical systems and probabilistic distributions with a high accuracy. It uses the same network repeatedly during a numerical integration. Hence, the backpropagation algorithm requires a memory footprint proportional to the number of uses times the network size. This is true even if a checkpointing scheme divides the computational graph into sub-graphs. Otherwise, the adjoint method obtains a gradient by a numerical integration backward in time with a minimal memory footprint; however, it suffers from numerical errors. This study proposes the symplectic adjoint method, which obtains the exact gradient (up to rounding error) with a footprint proportional to the number of uses plus the network size. The experimental results demonstrate the symplectic adjoint method occupies the smallest footprint in most cases, functions faster in some cases, and is robust to a rounding error among competitive methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge