Universal Approximation Properties of Neural Networks for Energy-Based Physical Systems

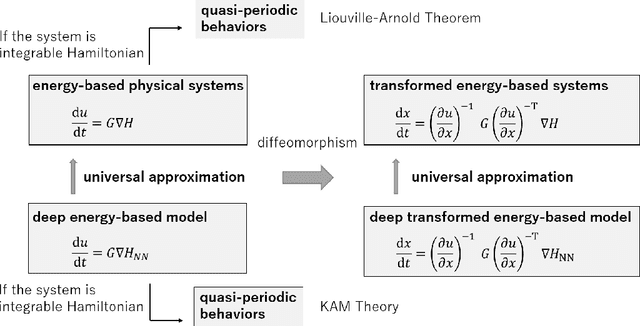
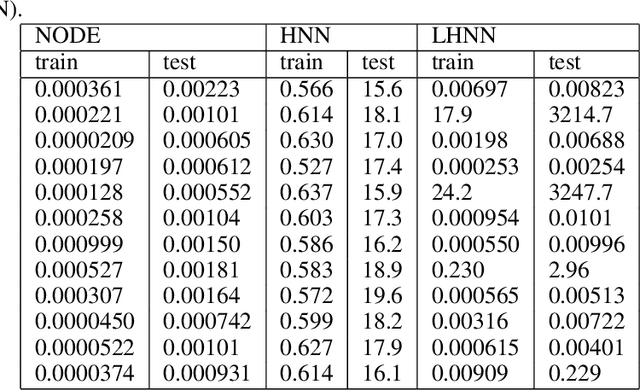
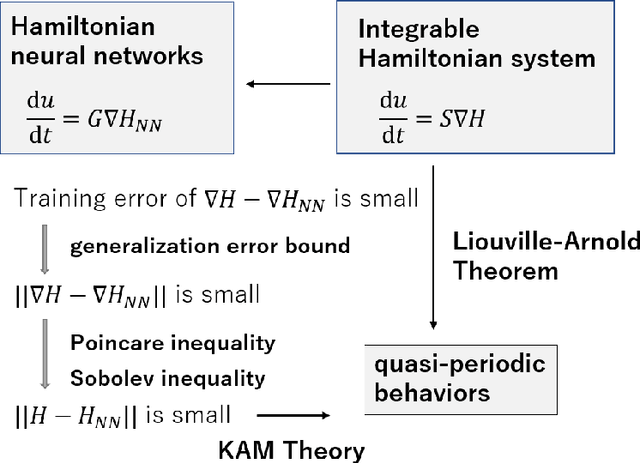
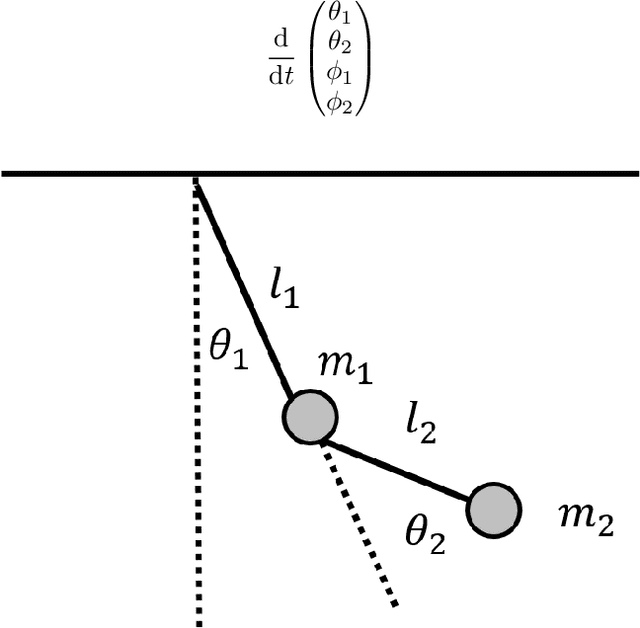
In Hamiltonian mechanics and the Landau theory, many physical phenomena are modeled using energy. In this paper, we prove the universal approximation property of neural network models for such physical phenomena. We also discuss behaviors of the models for integrable Hamiltonian systems when the loss function does not vanish completely by applying the KAM theory.