Structure-Preserving Physics-Informed Neural Networks With Energy or Lyapunov Structure

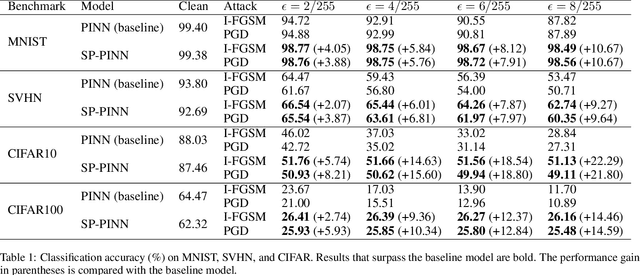
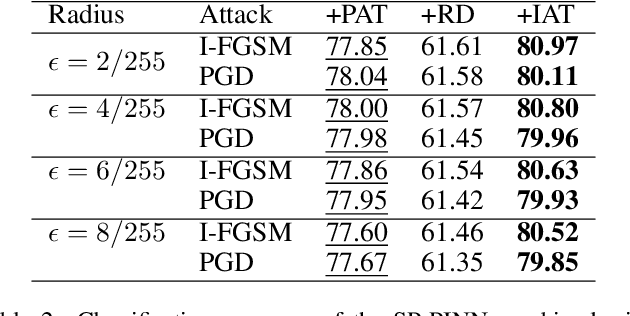
Recently, there has been growing interest in using physics-informed neural networks (PINNs) to solve differential equations. However, the preservation of structure, such as energy and stability, in a suitable manner has yet to be established. This limitation could be a potential reason why the learning process for PINNs is not always efficient and the numerical results may suggest nonphysical behavior. Besides, there is little research on their applications on downstream tasks. To address these issues, we propose structure-preserving PINNs to improve their performance and broaden their applications for downstream tasks. Firstly, by leveraging prior knowledge about the physical system, a structure-preserving loss function is designed to assist the PINN in learning the underlying structure. Secondly, a framework that utilizes structure-preserving PINN for robust image recognition is proposed. Here, preserving the Lyapunov structure of the underlying system ensures the stability of the system. Experimental results demonstrate that the proposed method improves the numerical accuracy of PINNs for partial differential equations. Furthermore, the robustness of the model against adversarial perturbations in image data is enhanced.

Learning Robust Deep Equilibrium Models

Deep equilibrium (DEQ) models have emerged as a promising class of implicit layer models in deep learning, which abandon traditional depth by solving for the fixed points of a single nonlinear layer. Despite their success, the stability of the fixed points for these models remains poorly understood. Recently, Lyapunov theory has been applied to Neural ODEs, another type of implicit layer model, to confer adversarial robustness. By considering DEQ models as nonlinear dynamic systems, we propose a robust DEQ model named LyaDEQ with guaranteed provable stability via Lyapunov theory. The crux of our method is ensuring the fixed points of the DEQ models are Lyapunov stable, which enables the LyaDEQ models to resist minor initial perturbations. To avoid poor adversarial defense due to Lyapunov-stable fixed points being located near each other, we add an orthogonal fully connected layer after the Lyapunov stability module to separate different fixed points. We evaluate LyaDEQ models on several widely used datasets under well-known adversarial attacks, and experimental results demonstrate significant improvement in robustness. Furthermore, we show that the LyaDEQ model can be combined with other defense methods, such as adversarial training, to achieve even better adversarial robustness.

Improving Neural ODEs via Knowledge Distillation

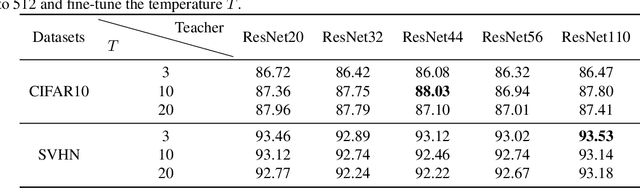
Neural Ordinary Differential Equations (Neural ODEs) construct the continuous dynamics of hidden units using ordinary differential equations specified by a neural network, demonstrating promising results on many tasks. However, Neural ODEs still do not perform well on image recognition tasks. The possible reason is that the one-hot encoding vector commonly used in Neural ODEs can not provide enough supervised information. We propose a new training based on knowledge distillation to construct more powerful and robust Neural ODEs fitting image recognition tasks. Specially, we model the training of Neural ODEs into a teacher-student learning process, in which we propose ResNets as the teacher model to provide richer supervised information. The experimental results show that the new training manner can improve the classification accuracy of Neural ODEs by 24% on CIFAR10 and 5% on SVHN. In addition, we also quantitatively discuss the effect of both knowledge distillation and time horizon in Neural ODEs on robustness against adversarial examples. The experimental analysis concludes that introducing the knowledge distillation and increasing the time horizon can improve the robustness of Neural ODEs against adversarial examples.

Towards Natural Robustness Against Adversarial Examples

Recent studies have shown that deep neural networks are vulnerable to adversarial examples, but most of the methods proposed to defense adversarial examples cannot solve this problem fundamentally. In this paper, we theoretically prove that there is an upper bound for neural networks with identity mappings to constrain the error caused by adversarial noises. However, in actual computations, this kind of neural network no longer holds any upper bound and is therefore susceptible to adversarial examples. Following similar procedures, we explain why adversarial examples can fool other deep neural networks with skip connections. Furthermore, we demonstrate that a new family of deep neural networks called Neural ODEs (Chen et al., 2018) holds a weaker upper bound. This weaker upper bound prevents the amount of change in the result from being too large. Thus, Neural ODEs have natural robustness against adversarial examples. We evaluate the performance of Neural ODEs compared with ResNet under three white-box adversarial attacks (FGSM, PGD, DI2-FGSM) and one black-box adversarial attack (Boundary Attack). Finally, we show that the natural robustness of Neural ODEs is even better than the robustness of neural networks that are trained with adversarial training methods, such as TRADES and YOPO.