Structure-Preserving Physics-Informed Neural Networks With Energy or Lyapunov Structure
Paper and Code
Jan 10, 2024
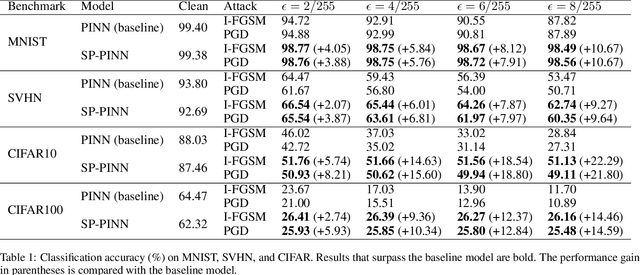

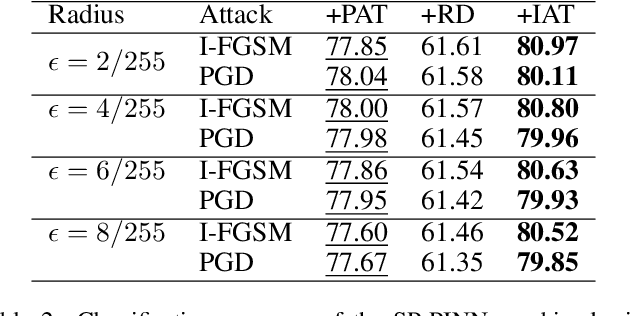
Recently, there has been growing interest in using physics-informed neural networks (PINNs) to solve differential equations. However, the preservation of structure, such as energy and stability, in a suitable manner has yet to be established. This limitation could be a potential reason why the learning process for PINNs is not always efficient and the numerical results may suggest nonphysical behavior. Besides, there is little research on their applications on downstream tasks. To address these issues, we propose structure-preserving PINNs to improve their performance and broaden their applications for downstream tasks. Firstly, by leveraging prior knowledge about the physical system, a structure-preserving loss function is designed to assist the PINN in learning the underlying structure. Secondly, a framework that utilizes structure-preserving PINN for robust image recognition is proposed. Here, preserving the Lyapunov structure of the underlying system ensures the stability of the system. Experimental results demonstrate that the proposed method improves the numerical accuracy of PINNs for partial differential equations. Furthermore, the robustness of the model against adversarial perturbations in image data is enhanced.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge