Evacuation Shelter Scheduling Problem

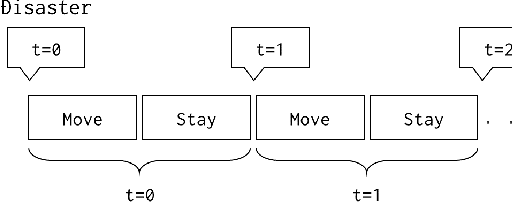
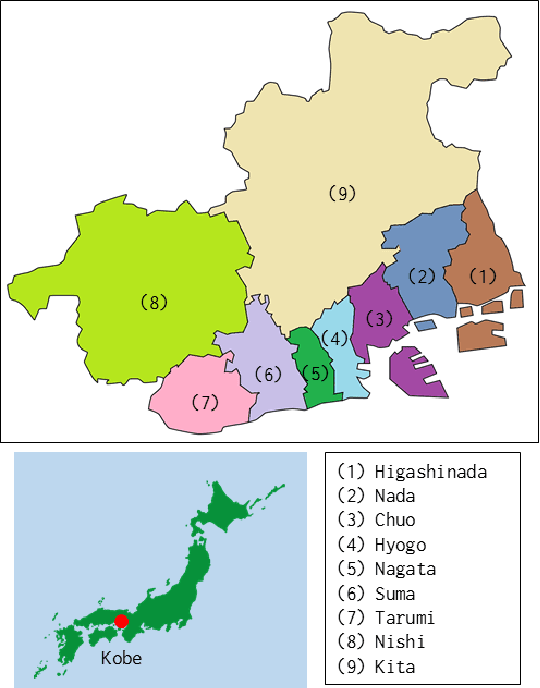
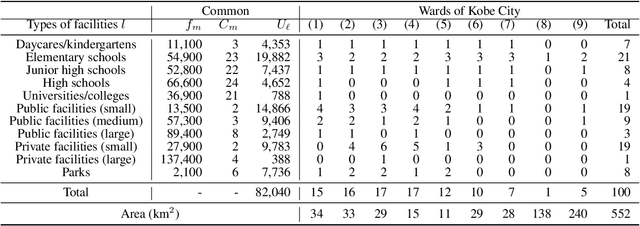
Evacuation shelters, which are urgently required during natural disasters, are designed to minimize the burden of evacuation on human survivors. However, the larger the scale of the disaster, the more costly it becomes to operate shelters. When the number of evacuees decreases, the operation costs can be reduced by moving the remaining evacuees to other shelters and closing shelters as quickly as possible. On the other hand, relocation between shelters imposes a huge emotional burden on evacuees. In this study, we formulate the "Evacuation Shelter Scheduling Problem," which allocates evacuees to shelters in such a way to minimize the movement costs of the evacuees and the operation costs of the shelters. Since it is difficult to solve this quadratic programming problem directly, we show its transformation into a 0-1 integer programming problem. In addition, such a formulation struggles to calculate the burden of relocating them from historical data because no payments are actually made. To solve this issue, we propose a method that estimates movement costs based on the numbers of evacuees and shelters during an actual disaster. Simulation experiments with records from the Kobe earthquake (Great Hanshin-Awaji Earthquake) showed that our proposed method reduced operation costs by 33.7 million dollars: 32%.

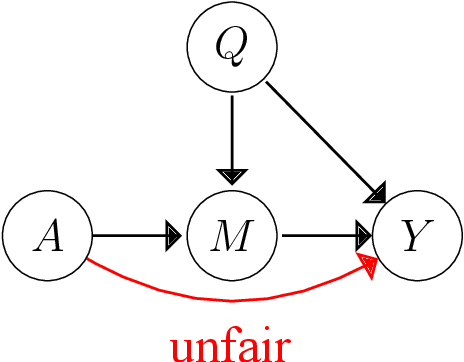
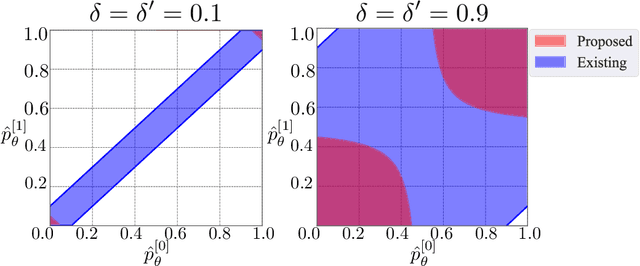
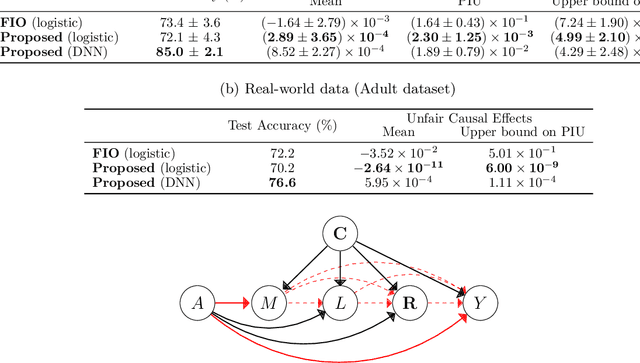
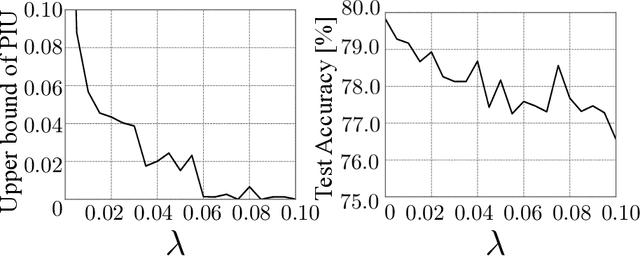
Learning Individually Fair Classifier with Causal-Effect Constraint

Machine learning is increasingly being used in various applications that make decisions for individuals. For such applications, we need to strike a balance between achieving good prediction accuracy and making fair decisions with respect to a sensitive feature (e.g., race or gender), which is difficult in complex real-world scenarios. Existing methods measure the unfairness in such scenarios as {\it unfair causal effects} and constrain its mean to zero. Unfortunately, with these methods, the decisions are not necessarily fair for all individuals because even when the mean unfair effect is zero, unfair effects might be positive for some individuals and negative for others, which is discriminatory for them. To learn a classifier that is fair for all individuals, we define unfairness as the {\it probability of individual unfairness} (PIU) and propose to solve an optimization problem that constrains an upper bound on PIU. We theoretically illustrate why our method achieves individual fairness. Experimental results demonstrate that our method learns an individually fair classifier at a slight cost of prediction accuracy.

Partial AUC Maximization via Nonlinear Scoring Functions

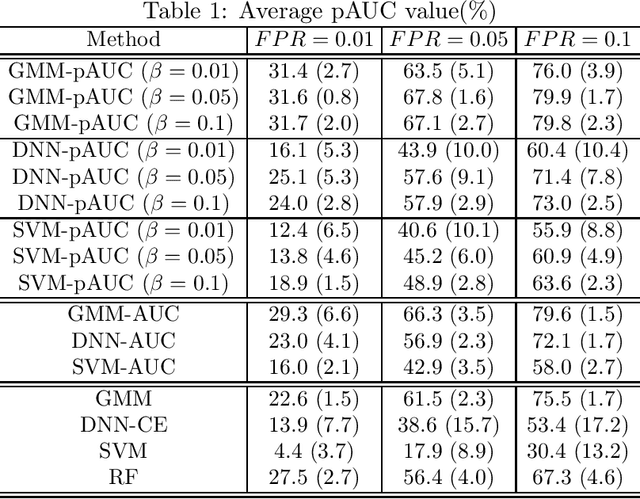
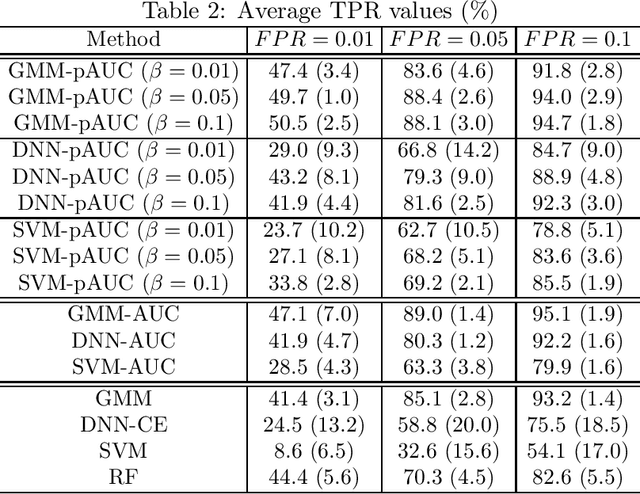
We propose a method for maximizing a partial area under a receiver operating characteristic (ROC) curve (pAUC) for binary classification tasks. In binary classification tasks, accuracy is the most commonly used as a measure of classifier performance. In some applications such as anomaly detection and diagnostic testing, accuracy is not an appropriate measure since prior probabilties are often greatly biased. Although in such cases the pAUC has been utilized as a performance measure, few methods have been proposed for directly maximizing the pAUC. This optimization is achieved by using a scoring function. The conventional approach utilizes a linear function as the scoring function. In contrast we newly introduce nonlinear scoring functions for this purpose. Specifically, we present two types of nonlinear scoring functions based on generative models and deep neural networks. We show experimentally that nonlinear scoring fucntions improve the conventional methods through the application of a binary classification of real and bogus objects obtained with the Hyper Suprime-Cam on the Subaru telescope.

Higher-Order Factorization Machines

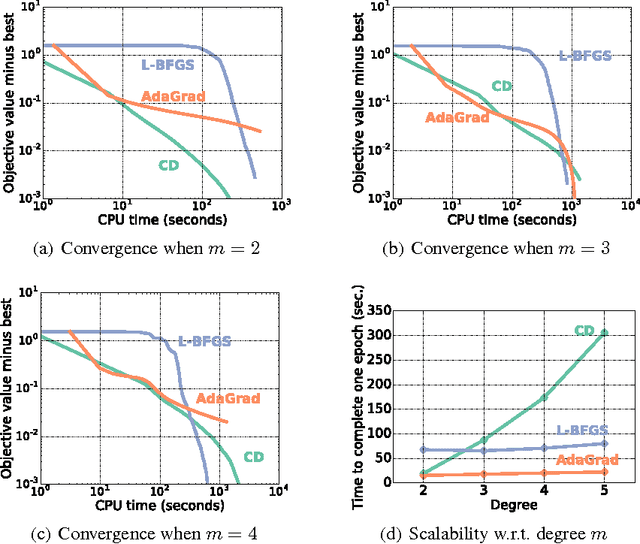
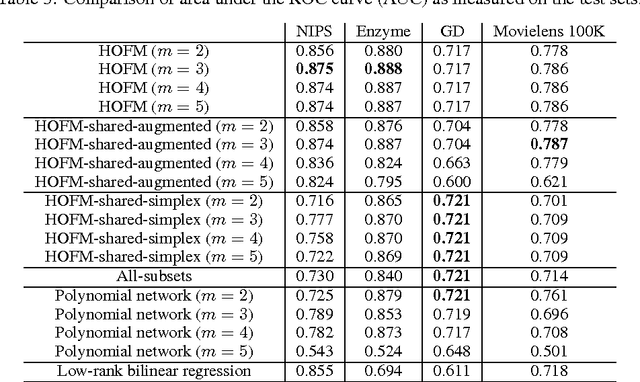
Factorization machines (FMs) are a supervised learning approach that can use second-order feature combinations even when the data is very high-dimensional. Unfortunately, despite increasing interest in FMs, there exists to date no efficient training algorithm for higher-order FMs (HOFMs). In this paper, we present the first generic yet efficient algorithms for training arbitrary-order HOFMs. We also present new variants of HOFMs with shared parameters, which greatly reduce model size and prediction times while maintaining similar accuracy. We demonstrate the proposed approaches on four different link prediction tasks.

Polynomial Networks and Factorization Machines: New Insights and Efficient Training Algorithms

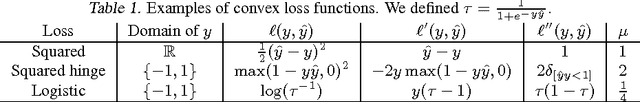
Polynomial networks and factorization machines are two recently-proposed models that can efficiently use feature interactions in classification and regression tasks. In this paper, we revisit both models from a unified perspective. Based on this new view, we study the properties of both models and propose new efficient training algorithms. Key to our approach is to cast parameter learning as a low-rank symmetric tensor estimation problem, which we solve by multi-convex optimization. We demonstrate our approach on regression and recommender system tasks.