Differentiable Pareto-Smoothed Weighting for High-Dimensional Heterogeneous Treatment Effect Estimation

There is a growing interest in estimating heterogeneous treatment effects across individuals using their high-dimensional feature attributes. Achieving high performance in such high-dimensional heterogeneous treatment effect estimation is challenging because in this setup, it is usual that some features induce sample selection bias while others do not but are predictive of potential outcomes. To avoid losing such predictive feature information, existing methods learn separate feature representations using the inverse of probability weighting (IPW). However, due to the numerically unstable IPW weights, they suffer from estimation bias under a finite sample setup. To develop a numerically robust estimator via weighted representation learning, we propose a differentiable Pareto-smoothed weighting framework that replaces extreme weight values in an end-to-end fashion. Experimental results show that by effectively correcting the weight values, our method outperforms the existing ones, including traditional weighting schemes.

Uncertainty Quantification in Heterogeneous Treatment Effect Estimation with Gaussian-Process-Based Partially Linear Model

Estimating heterogeneous treatment effects across individuals has attracted growing attention as a statistical tool for performing critical decision-making. We propose a Bayesian inference framework that quantifies the uncertainty in treatment effect estimation to support decision-making in a relatively small sample size setting. Our proposed model places Gaussian process priors on the nonparametric components of a semiparametric model called a partially linear model. This model formulation has three advantages. First, we can analytically compute the posterior distribution of a treatment effect without relying on the computationally demanding posterior approximation. Second, we can guarantee that the posterior distribution concentrates around the true one as the sample size goes to infinity. Third, we can incorporate prior knowledge about a treatment effect into the prior distribution, improving the estimation efficiency. Our experimental results show that even in the small sample size setting, our method can accurately estimate the heterogeneous treatment effects and effectively quantify its estimation uncertainty.

Meta-learning for heterogeneous treatment effect estimation with closed-form solvers

This article proposes a meta-learning method for estimating the conditional average treatment effect (CATE) from a few observational data. The proposed method learns how to estimate CATEs from multiple tasks and uses the knowledge for unseen tasks. In the proposed method, based on the meta-learner framework, we decompose the CATE estimation problem into sub-problems. For each sub-problem, we formulate our estimation models using neural networks with task-shared and task-specific parameters. With our formulation, we can obtain optimal task-specific parameters in a closed form that are differentiable with respect to task-shared parameters, making it possible to perform effective meta-learning. The task-shared parameters are trained such that the expected CATE estimation performance in few-shot settings is improved by minimizing the difference between a CATE estimated with a large amount of data and one estimated with just a few data. Our experimental results demonstrate that our method outperforms the existing meta-learning approaches and CATE estimation methods.

Feature Selection for Discovering Distributional Treatment Effect Modifiers

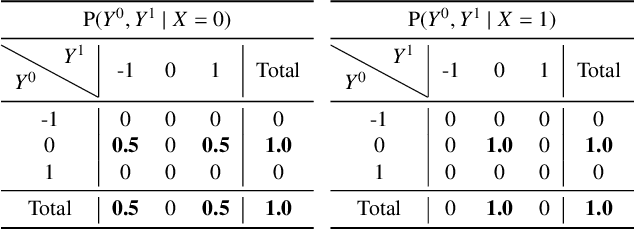
Finding the features relevant to the difference in treatment effects is essential to unveil the underlying causal mechanisms. Existing methods seek such features by measuring how greatly the feature attributes affect the degree of the {\it conditional average treatment effect} (CATE). However, these methods may overlook important features because CATE, a measure of the average treatment effect, cannot detect differences in distribution parameters other than the mean (e.g., variance). To resolve this weakness of existing methods, we propose a feature selection framework for discovering {\it distributional treatment effect modifiers}. We first formulate a feature importance measure that quantifies how strongly the feature attributes influence the discrepancy between potential outcome distributions. Then we derive its computationally efficient estimator and develop a feature selection algorithm that can control the type I error rate to the desired level. Experimental results show that our framework successfully discovers important features and outperforms the existing mean-based method.

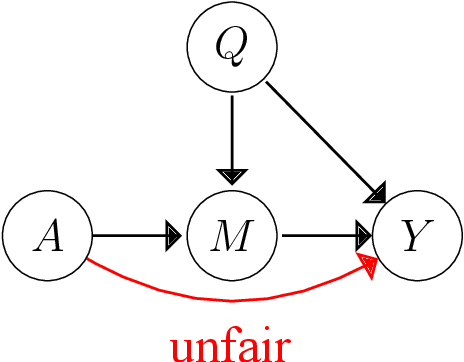
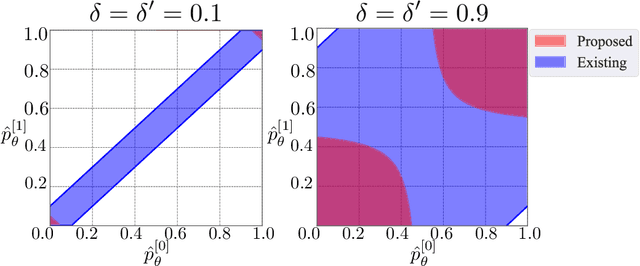
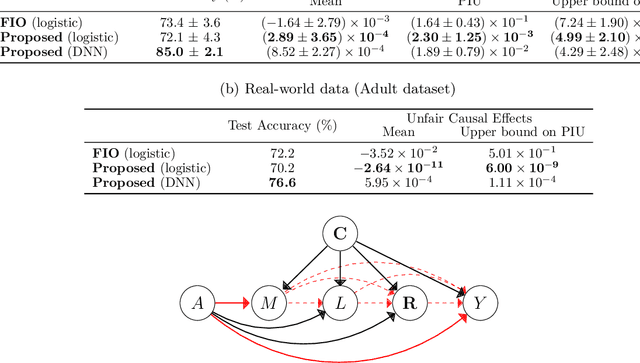
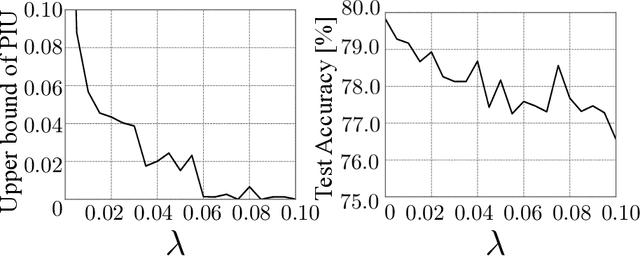
Learning Individually Fair Classifier with Causal-Effect Constraint

Machine learning is increasingly being used in various applications that make decisions for individuals. For such applications, we need to strike a balance between achieving good prediction accuracy and making fair decisions with respect to a sensitive feature (e.g., race or gender), which is difficult in complex real-world scenarios. Existing methods measure the unfairness in such scenarios as {\it unfair causal effects} and constrain its mean to zero. Unfortunately, with these methods, the decisions are not necessarily fair for all individuals because even when the mean unfair effect is zero, unfair effects might be positive for some individuals and negative for others, which is discriminatory for them. To learn a classifier that is fair for all individuals, we define unfairness as the {\it probability of individual unfairness} (PIU) and propose to solve an optimization problem that constrains an upper bound on PIU. We theoretically illustrate why our method achieves individual fairness. Experimental results demonstrate that our method learns an individually fair classifier at a slight cost of prediction accuracy.