DAG Learning from Zero-Inflated Count Data Using Continuous Optimization

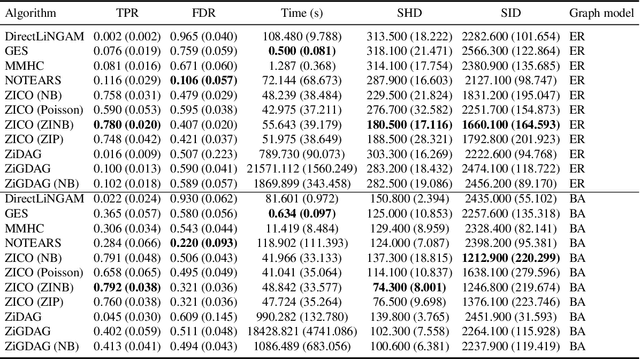
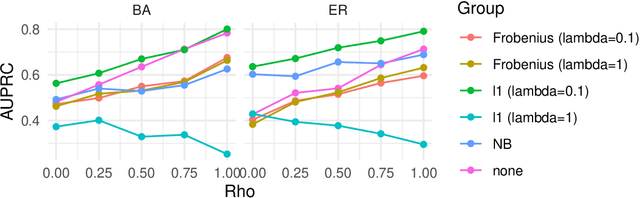
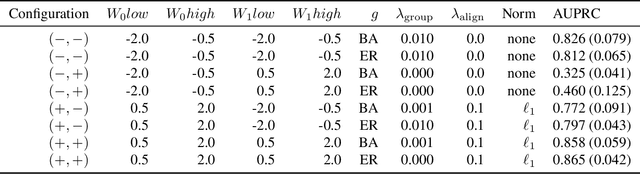
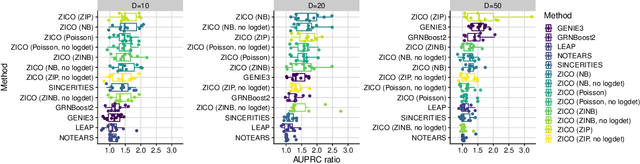
We address network structure learning from zero-inflated count data by casting each node as a zero-inflated generalized linear model and optimizing a smooth, score-based objective under a directed acyclic graph constraint. Our Zero-Inflated Continuous Optimization (ZICO) approach uses node-wise likelihoods with canonical links and enforces acyclicity through a differentiable surrogate constraint combined with sparsity regularization. ZICO achieves superior performance with faster runtimes on simulated data. It also performs comparably to or better than common algorithms for reverse engineering gene regulatory networks. ZICO is fully vectorized and mini-batched, enabling learning on larger variable sets with practical runtimes in a wide range of domains.

Practical Causal Evaluation Metrics for Biological Networks

Estimating causal networks from biological data is a critical step in systems biology. When evaluating the inferred network, assessing the networks based on their intervention effects is particularly important for downstream probabilistic reasoning and the identification of potential drug targets. In the context of gene regulatory network inference, biological databases are often used as reference sources. These databases typically describe relationships in a qualitative rather than quantitative manner. However, few evaluation metrics have been developed that take this qualitative nature into account. To address this, we developed a metric, the sign-augmented Structural Intervention Distance (sSID), and a weighted sSID that incorporates the net effects of the intervention. Through simulations and analyses of real transcriptomic datasets, we found that our proposed metrics could identify a different algorithm as optimal compared to conventional metrics, and the network selected by sSID had a superior performance in the classification task of clinical covariates using transcriptomic data. This suggests that sSID can distinguish networks that are structurally correct but functionally incorrect, highlighting its potential as a more biologically meaningful and practical evaluation metric.

Linear Tensor Projection Revealing Nonlinearity

Dimensionality reduction is an effective method for learning high-dimensional data, which can provide better understanding of decision boundaries in human-readable low-dimensional subspace. Linear methods, such as principal component analysis and linear discriminant analysis, make it possible to capture the correlation between many variables; however, there is no guarantee that the correlations that are important in predicting data can be captured. Moreover, if the decision boundary has strong nonlinearity, the guarantee becomes increasingly difficult. This problem is exacerbated when the data are matrices or tensors that represent relationships between variables. We propose a learning method that searches for a subspace that maximizes the prediction accuracy while retaining as much of the original data information as possible, even if the prediction model in the subspace has strong nonlinearity. This makes it easier to interpret the mechanism of the group of variables behind the prediction problem that the user wants to know. We show the effectiveness of our method by applying it to various types of data including matrices and tensors.