Dataset Dictionary Learning in a Wasserstein Space for Federated Domain Adaptation

Multi-Source Domain Adaptation (MSDA) is a challenging scenario where multiple related and heterogeneous source datasets must be adapted to an unlabeled target dataset. Conventional MSDA methods often overlook that data holders may have privacy concerns, hindering direct data sharing. In response, decentralized MSDA has emerged as a promising strategy to achieve adaptation without centralizing clients' data. Our work proposes a novel approach, Decentralized Dataset Dictionary Learning, to address this challenge. Our method leverages Wasserstein barycenters to model the distributional shift across multiple clients, enabling effective adaptation while preserving data privacy. Specifically, our algorithm expresses each client's underlying distribution as a Wasserstein barycenter of public atoms, weighted by private barycentric coordinates. Our approach ensures that the barycentric coordinates remain undisclosed throughout the adaptation process. Extensive experimentation across five visual domain adaptation benchmarks demonstrates the superiority of our strategy over existing decentralized MSDA techniques. Moreover, our method exhibits enhanced robustness to client parallelism while maintaining relative resilience compared to conventional decentralized MSDA methodologies.

When approximate design for fast homomorphic computation provides differential privacy guarantees

While machine learning has become pervasive in as diversified fields as industry, healthcare, social networks, privacy concerns regarding the training data have gained a critical importance. In settings where several parties wish to collaboratively train a common model without jeopardizing their sensitive data, the need for a private training protocol is particularly stringent and implies to protect the data against both the model's end-users and the actors of the training phase. Differential privacy (DP) and cryptographic primitives are complementary popular countermeasures against privacy attacks. Among these cryptographic primitives, fully homomorphic encryption (FHE) offers ciphertext malleability at the cost of time-consuming operations in the homomorphic domain. In this paper, we design SHIELD, a probabilistic approximation algorithm for the argmax operator which is both fast when homomorphically executed and whose inaccuracy is used as a feature to ensure DP guarantees. Even if SHIELD could have other applications, we here focus on one setting and seamlessly integrate it in the SPEED collaborative training framework from "SPEED: Secure, PrivatE, and Efficient Deep learning" (Grivet S\'ebert et al., 2021) to improve its computational efficiency. After thoroughly describing the FHE implementation of our algorithm and its DP analysis, we present experimental results. To the best of our knowledge, it is the first work in which relaxing the accuracy of an homomorphic calculation is constructively usable as a degree of freedom to achieve better FHE performances.

Protecting Data from all Parties: Combining FHE and DP in Federated Learning

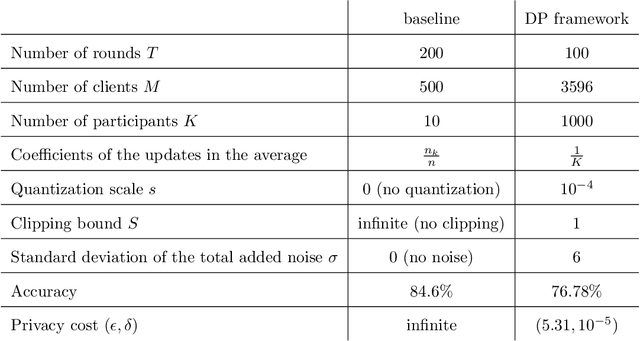
This paper tackles the problem of ensuring training data privacy in a federated learning context. Relying on Fully Homomorphic Encryption (FHE) and Differential Privacy (DP), we propose a secure framework addressing an extended threat model with respect to privacy of the training data. Notably, the proposed framework protects the privacy of the training data from all participants, namely the training data owners and an aggregating server. In details, while homomorphic encryption blinds a semi-honest server at learning stage, differential privacy protects the data from semi-honest clients participating in the training process as well as curious end-users with black-box or white-box access to the trained model. This paper provides with new theoretical and practical results to enable these techniques to be effectively combined. In particular, by means of a novel stochastic quantization operator, we prove differential privacy guarantees in a context where the noise is quantified and bounded due to the use of homomorphic encryption. The paper is concluded by experiments which show the practicality of the entire framework in spite of these interferences in terms of both model quality (impacted by DP) and computational overheads (impacted by FHE).

On the robustness of randomized classifiers to adversarial examples

This paper investigates the theory of robustness against adversarial attacks. We focus on randomized classifiers (\emph{i.e.} classifiers that output random variables) and provide a thorough analysis of their behavior through the lens of statistical learning theory and information theory. To this aim, we introduce a new notion of robustness for randomized classifiers, enforcing local Lipschitzness using probability metrics. Equipped with this definition, we make two new contributions. The first one consists in devising a new upper bound on the adversarial generalization gap of randomized classifiers. More precisely, we devise bounds on the generalization gap and the adversarial gap (\emph{i.e.} the gap between the risk and the worst-case risk under attack) of randomized classifiers. The second contribution presents a yet simple but efficient noise injection method to design robust randomized classifiers. We show that our results are applicable to a wide range of machine learning models under mild hypotheses. We further corroborate our findings with experimental results using deep neural networks on standard image datasets, namely CIFAR-10 and CIFAR-100. All robust models we trained models can simultaneously achieve state-of-the-art accuracy (over $0.82$ clean accuracy on CIFAR-10) and enjoy \emph{guaranteed} robust accuracy bounds ($0.45$ against $\ell_2$ adversaries with magnitude $0.5$ on CIFAR-10).

SPEED: Secure, PrivatE, and Efficient Deep learning

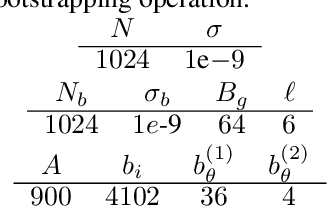
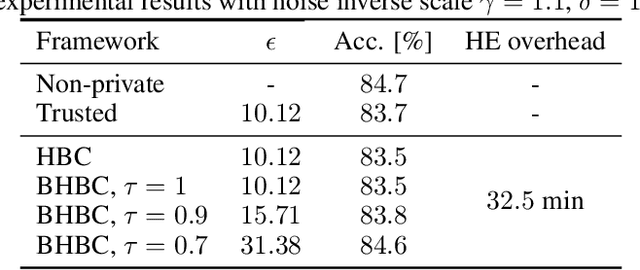
This paper addresses the issue of collaborative deep learning with privacy constraints. Building upon differentially private decentralized semi-supervised learning, we introduce homomorphically encrypted operations to extend the set of threats considered so far. While previous methods relied on the existence of an hypothetical 'trusted' third party, we designed specific aggregation operations in the encrypted domain that allow us to circumvent this assumption. This makes our method practical to real-life scenario where data holders do not trust any third party to process their datasets. Crucially the computational burden of the approach is maintained reasonable, making it suitable to deep learning applications. In order to illustrate the performances of our method, we carried out numerical experiments using image datasets in a classification context.

A unified view on differential privacy and robustness to adversarial examples

This short note highlights some links between two lines of research within the emerging topic of trustworthy machine learning: differential privacy and robustness to adversarial examples. By abstracting the definitions of both notions, we show that they build upon the same theoretical ground and hence results obtained so far in one domain can be transferred to the other. More precisely, our analysis is based on two key elements: probabilistic mappings (also called randomized algorithms in the differential privacy community), and the Renyi divergence which subsumes a large family of divergences. We first generalize the definition of robustness against adversarial examples to encompass probabilistic mappings. Then we observe that Renyi-differential privacy (a generalization of differential privacy recently proposed in~\cite{Mironov2017RenyiDP}) and our definition of robustness share several similarities. We finally discuss how can both communities benefit from this connection to transfer technical tools from one research field to the other.

Theoretical evidence for adversarial robustness through randomization: the case of the Exponential family

This paper investigates the theory of robustness against adversarial attacks. It focuses on the family of randomization techniques that consist in injecting noise in the network at inference time. These techniques have proven effective in many contexts, but lack theoretical arguments. We close this gap by presenting a theoretical analysis of these approaches, hence explaining why they perform well in practice. More precisely, we provide the first result relating the randomization rate to robustness to adversarial attacks. This result applies for the general family of exponential distributions, and thus extends and unifies the previous approaches. We support our theoretical claims with a set of experiments.

Graph sketching-based Space-efficient Data Clustering

In this paper, we address the problem of recovering arbitrary-shaped data clusters from datasets while facing \emph{high space constraints}, as this is for instance the case in many real-world applications when analysis algorithms are directly deployed on resources-limited mobile devices collecting the data. We present DBMSTClu a new space-efficient density-based \emph{non-parametric} method working on a Minimum Spanning Tree (MST) recovered from a limited number of linear measurements i.e. a \emph{sketched} version of the dissimilarity graph $\mathcal{G}$ between the $N$ objects to cluster. Unlike $k$-means, $k$-medians or $k$-medoids algorithms, it does not fail at distinguishing clusters with particular forms thanks to the property of the MST for expressing the underlying structure of a graph. No input parameter is needed contrarily to DBSCAN or the Spectral Clustering method. An approximate MST is retrieved by following the dynamic \emph{semi-streaming} model in handling the dissimilarity graph $\mathcal{G}$ as a stream of edge weight updates which is sketched in one pass over the data into a compact structure requiring $O(N \operatorname{polylog}(N))$ space, far better than the theoretical memory cost $O(N^2)$ of $\mathcal{G}$. The recovered approximate MST $\mathcal{T}$ as input, DBMSTClu then successfully detects the right number of nonconvex clusters by performing relevant cuts on $\mathcal{T}$ in a time linear in $N$. We provide theoretical guarantees on the quality of the clustering partition and also demonstrate its advantage over the existing state-of-the-art on several datasets.

Graph-based Clustering under Differential Privacy

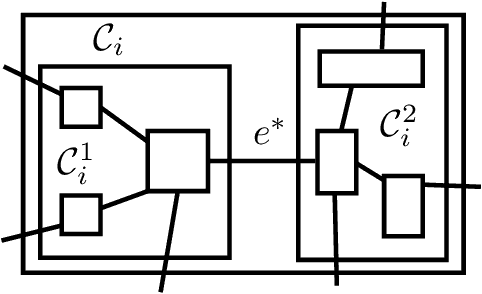
In this paper, we present the first differentially private clustering method for arbitrary-shaped node clusters in a graph. This algorithm takes as input only an approximate Minimum Spanning Tree (MST) $\mathcal{T}$ released under weight differential privacy constraints from the graph. Then, the underlying nonconvex clustering partition is successfully recovered from cutting optimal cuts on $\mathcal{T}$. As opposed to existing methods, our algorithm is theoretically well-motivated. Experiments support our theoretical findings.

On the Needs for Rotations in Hypercubic Quantization Hashing

The aim of this paper is to endow the well-known family of hypercubic quantization hashing methods with theoretical guarantees. In hypercubic quantization, applying a suitable (random or learned) rotation after dimensionality reduction has been experimentally shown to improve the results accuracy in the nearest neighbors search problem. We prove in this paper that the use of these rotations is optimal under some mild assumptions: getting optimal binary sketches is equivalent to applying a rotation uniformizing the diagonal of the covariance matrix between data points. Moreover, for two closed points, the probability to have dissimilar binary sketches is upper bounded by a factor of the initial distance between the data points. Relaxing these assumptions, we obtain a general concentration result for random matrices. We also provide some experiments illustrating these theoretical points and compare a set of algorithms in both the batch and online settings.