Graph-based Clustering under Differential Privacy
Paper and Code
Mar 10, 2018

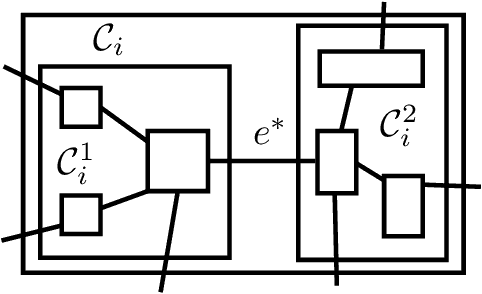
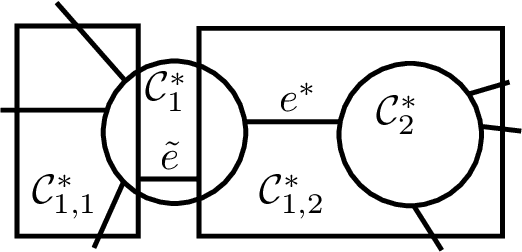
In this paper, we present the first differentially private clustering method for arbitrary-shaped node clusters in a graph. This algorithm takes as input only an approximate Minimum Spanning Tree (MST) $\mathcal{T}$ released under weight differential privacy constraints from the graph. Then, the underlying nonconvex clustering partition is successfully recovered from cutting optimal cuts on $\mathcal{T}$. As opposed to existing methods, our algorithm is theoretically well-motivated. Experiments support our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge