Graph sketching-based Space-efficient Data Clustering

In this paper, we address the problem of recovering arbitrary-shaped data clusters from datasets while facing \emph{high space constraints}, as this is for instance the case in many real-world applications when analysis algorithms are directly deployed on resources-limited mobile devices collecting the data. We present DBMSTClu a new space-efficient density-based \emph{non-parametric} method working on a Minimum Spanning Tree (MST) recovered from a limited number of linear measurements i.e. a \emph{sketched} version of the dissimilarity graph $\mathcal{G}$ between the $N$ objects to cluster. Unlike $k$-means, $k$-medians or $k$-medoids algorithms, it does not fail at distinguishing clusters with particular forms thanks to the property of the MST for expressing the underlying structure of a graph. No input parameter is needed contrarily to DBSCAN or the Spectral Clustering method. An approximate MST is retrieved by following the dynamic \emph{semi-streaming} model in handling the dissimilarity graph $\mathcal{G}$ as a stream of edge weight updates which is sketched in one pass over the data into a compact structure requiring $O(N \operatorname{polylog}(N))$ space, far better than the theoretical memory cost $O(N^2)$ of $\mathcal{G}$. The recovered approximate MST $\mathcal{T}$ as input, DBMSTClu then successfully detects the right number of nonconvex clusters by performing relevant cuts on $\mathcal{T}$ in a time linear in $N$. We provide theoretical guarantees on the quality of the clustering partition and also demonstrate its advantage over the existing state-of-the-art on several datasets.

Graph-based Clustering under Differential Privacy

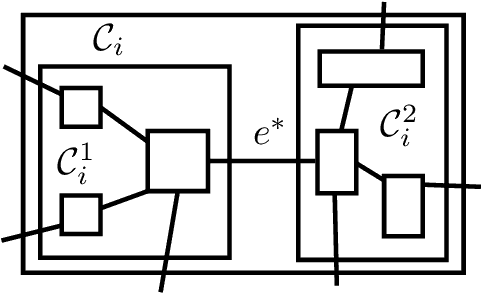
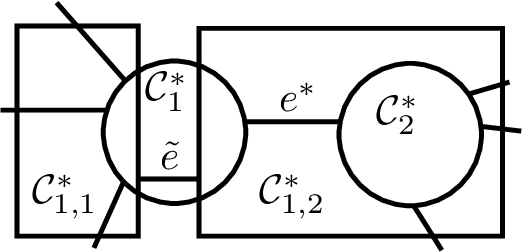
In this paper, we present the first differentially private clustering method for arbitrary-shaped node clusters in a graph. This algorithm takes as input only an approximate Minimum Spanning Tree (MST) $\mathcal{T}$ released under weight differential privacy constraints from the graph. Then, the underlying nonconvex clustering partition is successfully recovered from cutting optimal cuts on $\mathcal{T}$. As opposed to existing methods, our algorithm is theoretically well-motivated. Experiments support our theoretical findings.

On the Needs for Rotations in Hypercubic Quantization Hashing

The aim of this paper is to endow the well-known family of hypercubic quantization hashing methods with theoretical guarantees. In hypercubic quantization, applying a suitable (random or learned) rotation after dimensionality reduction has been experimentally shown to improve the results accuracy in the nearest neighbors search problem. We prove in this paper that the use of these rotations is optimal under some mild assumptions: getting optimal binary sketches is equivalent to applying a rotation uniformizing the diagonal of the covariance matrix between data points. Moreover, for two closed points, the probability to have dissimilar binary sketches is upper bounded by a factor of the initial distance between the data points. Relaxing these assumptions, we obtain a general concentration result for random matrices. We also provide some experiments illustrating these theoretical points and compare a set of algorithms in both the batch and online settings.

Streaming Binary Sketching based on Subspace Tracking and Diagonal Uniformization

In this paper, we address the problem of learning compact similarity-preserving embeddings for massive high-dimensional streams of data in order to perform efficient similarity search. We present a new online method for computing binary compressed representations -sketches- of high-dimensional real feature vectors. Given an expected code length $c$ and high-dimensional input data points, our algorithm provides a $c$-bits binary code for preserving the distance between the points from the original high-dimensional space. Our algorithm does not require neither the storage of the whole dataset nor a chunk, thus it is fully adaptable to the streaming setting. It also provides low time complexity and convergence guarantees. We demonstrate the quality of our binary sketches through experiments on real data for the nearest neighbors search task in the online setting.

Structured adaptive and random spinners for fast machine learning computations

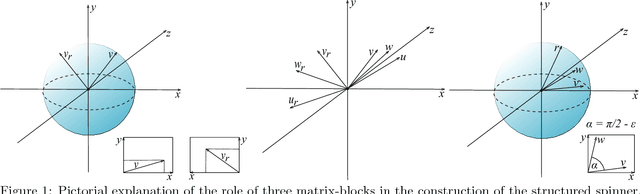
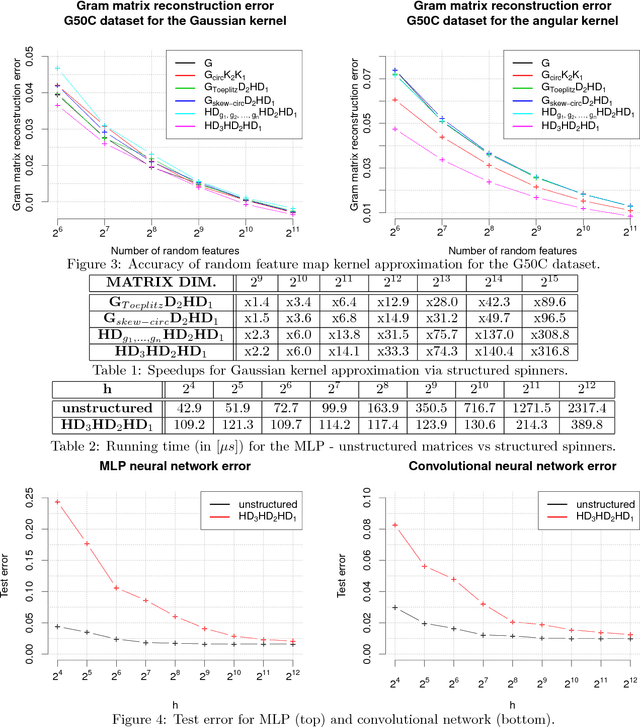
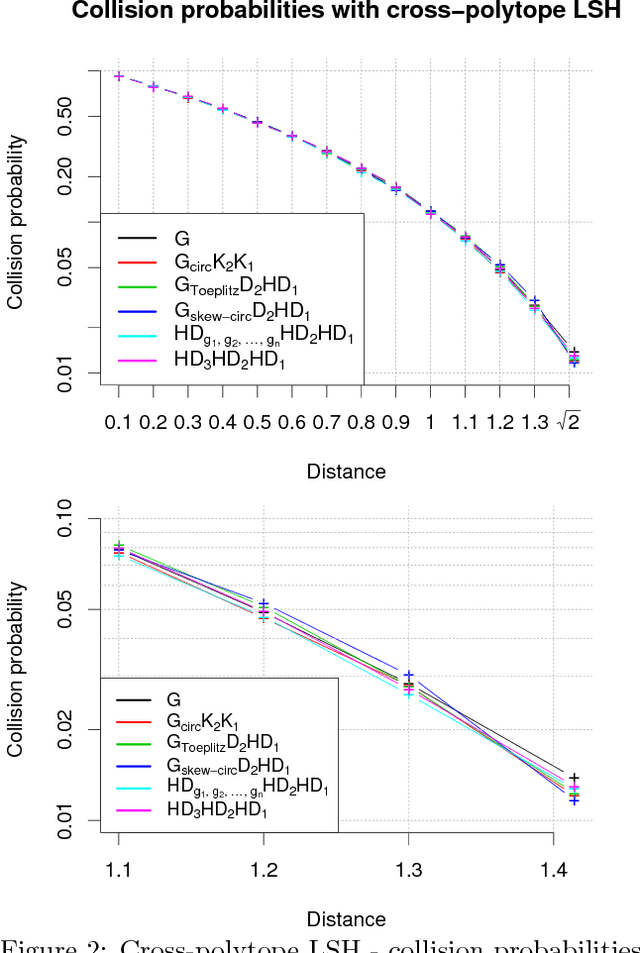
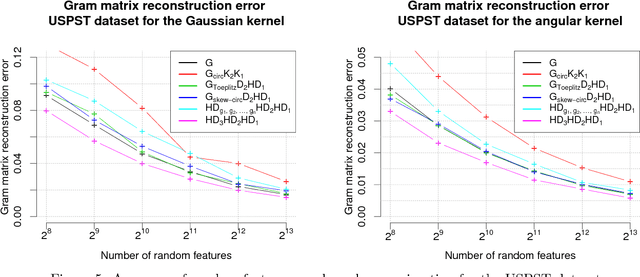
We consider an efficient computational framework for speeding up several machine learning algorithms with almost no loss of accuracy. The proposed framework relies on projections via structured matrices that we call Structured Spinners, which are formed as products of three structured matrix-blocks that incorporate rotations. The approach is highly generic, i.e. i) structured matrices under consideration can either be fully-randomized or learned, ii) our structured family contains as special cases all previously considered structured schemes, iii) the setting extends to the non-linear case where the projections are followed by non-linear functions, and iv) the method finds numerous applications including kernel approximations via random feature maps, dimensionality reduction algorithms, new fast cross-polytope LSH techniques, deep learning, convex optimization algorithms via Newton sketches, quantization with random projection trees, and more. The proposed framework comes with theoretical guarantees characterizing the capacity of the structured model in reference to its unstructured counterpart and is based on a general theoretical principle that we describe in the paper. As a consequence of our theoretical analysis, we provide the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the HD3HD2HD1 structured matrix [Andoni et al., 2015]. The exhaustive experimental evaluation confirms the accuracy and efficiency of structured spinners for a variety of different applications.

TripleSpin - a generic compact paradigm for fast machine learning computations

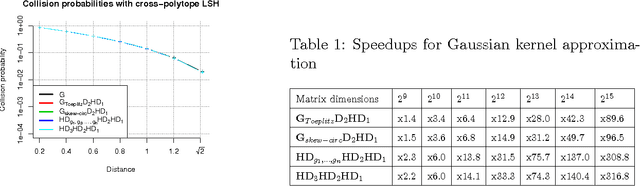
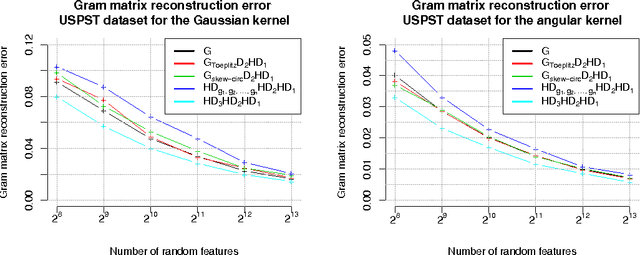
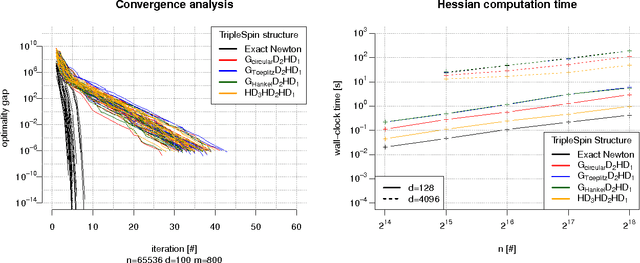
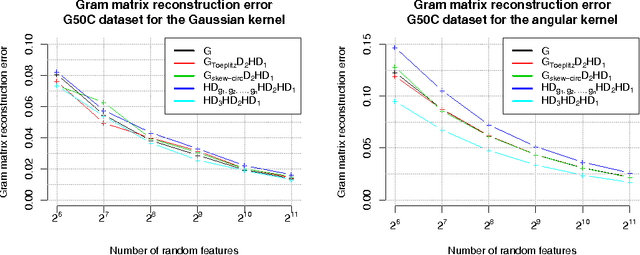
We present a generic compact computational framework relying on structured random matrices that can be applied to speed up several machine learning algorithms with almost no loss of accuracy. The applications include new fast LSH-based algorithms, efficient kernel computations via random feature maps, convex optimization algorithms, quantization techniques and many more. Certain models of the presented paradigm are even more compressible since they apply only bit matrices. This makes them suitable for deploying on mobile devices. All our findings come with strong theoretical guarantees. In particular, as a byproduct of the presented techniques and by using relatively new Berry-Esseen-type CLT for random vectors, we give the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the $\textbf{HD}_{3}\textbf{HD}_{2}\textbf{HD}_{1}$ structured matrix ("Practical and Optimal LSH for Angular Distance"). These guarantees as well as theoretical results for other aforementioned applications follow from the same general theoretical principle that we present in the paper. Our structured family contains as special cases all previously considered structured schemes, including the recently introduced $P$-model. Experimental evaluation confirms the accuracy and efficiency of TripleSpin matrices.