A Survey of Optimization Methods for Training DL Models: Theoretical Perspective on Convergence and Generalization

As data sets grow in size and complexity, it is becoming more difficult to pull useful features from them using hand-crafted feature extractors. For this reason, deep learning (DL) frameworks are now widely popular. The Holy Grail of DL and one of the most mysterious challenges in all of modern ML is to develop a fundamental understanding of DL optimization and generalization. While numerous optimization techniques have been introduced in the literature to navigate the exploration of the highly non-convex DL optimization landscape, many survey papers reviewing them primarily focus on summarizing these methodologies, often overlooking the critical theoretical analyses of these methods. In this paper, we provide an extensive summary of the theoretical foundations of optimization methods in DL, including presenting various methodologies, their convergence analyses, and generalization abilities. This paper not only includes theoretical analysis of popular generic gradient-based first-order and second-order methods, but it also covers the analysis of the optimization techniques adapting to the properties of the DL loss landscape and explicitly encouraging the discovery of well-generalizing optimal points. Additionally, we extend our discussion to distributed optimization methods that facilitate parallel computations, including both centralized and decentralized approaches. We provide both convex and non-convex analysis for the optimization algorithms considered in this survey paper. Finally, this paper aims to serve as a comprehensive theoretical handbook on optimization methods for DL, offering insights and understanding to both novice and seasoned researchers in the field.

AD-L-JEPA: Self-Supervised Spatial World Models with Joint Embedding Predictive Architecture for Autonomous Driving with LiDAR Data

As opposed to human drivers, current autonomous driving systems still require vast amounts of labeled data to train. Recently, world models have been proposed to simultaneously enhance autonomous driving capabilities by improving the way these systems understand complex real-world environments and reduce their data demands via self-supervised pre-training. In this paper, we present AD-L-JEPA (aka Autonomous Driving with LiDAR data via a Joint Embedding Predictive Architecture), a novel self-supervised pre-training framework for autonomous driving with LiDAR data that, as opposed to existing methods, is neither generative nor contrastive. Our method learns spatial world models with a joint embedding predictive architecture. Instead of explicitly generating masked unknown regions, our self-supervised world models predict Bird's Eye View (BEV) embeddings to represent the diverse nature of autonomous driving scenes. Our approach furthermore eliminates the need to manually create positive and negative pairs, as is the case in contrastive learning. AD-L-JEPA leads to simpler implementation and enhanced learned representations. We qualitatively and quantitatively demonstrate high-quality of embeddings learned with AD-L-JEPA. We furthermore evaluate the accuracy and label efficiency of AD-L-JEPA on popular downstream tasks such as LiDAR 3D object detection and associated transfer learning. Our experimental evaluation demonstrates that AD-L-JEPA is a plausible approach for self-supervised pre-training in autonomous driving applications and is the best available approach outperforming SOTA, including most recently proposed Occupancy-MAE [1] and ALSO [2]. The source code of AD-L-JEPA is available at https://github.com/HaoranZhuExplorer/AD-L-JEPA-Release.

Adjacent Leader Decentralized Stochastic Gradient Descent

This work focuses on the decentralized deep learning optimization framework. We propose Adjacent Leader Decentralized Gradient Descent (AL-DSGD), for improving final model performance, accelerating convergence, and reducing the communication overhead of decentralized deep learning optimizers. AL-DSGD relies on two main ideas. Firstly, to increase the influence of the strongest learners on the learning system it assigns weights to different neighbor workers according to both their performance and the degree when averaging among them, and it applies a corrective force on the workers dictated by both the currently best-performing neighbor and the neighbor with the maximal degree. Secondly, to alleviate the problem of the deterioration of the convergence speed and performance of the nodes with lower degrees, AL-DSGD relies on dynamic communication graphs, which effectively allows the workers to communicate with more nodes while keeping the degrees of the nodes low. Experiments demonstrate that AL-DSGD accelerates the convergence of the decentralized state-of-the-art techniques and improves their test performance especially in the communication constrained environments. We also theoretically prove the convergence of the proposed scheme. Finally, we release to the community a highly general and concise PyTorch-based library for distributed training of deep learning models that supports easy implementation of any distributed deep learning approach ((a)synchronous, (de)centralized).

GRAWA: Gradient-based Weighted Averaging for Distributed Training of Deep Learning Models

We study distributed training of deep learning models in time-constrained environments. We propose a new algorithm that periodically pulls workers towards the center variable computed as a weighted average of workers, where the weights are inversely proportional to the gradient norms of the workers such that recovering the flat regions in the optimization landscape is prioritized. We develop two asynchronous variants of the proposed algorithm that we call Model-level and Layer-level Gradient-based Weighted Averaging (resp. MGRAWA and LGRAWA), which differ in terms of the weighting scheme that is either done with respect to the entire model or is applied layer-wise. On the theoretical front, we prove the convergence guarantee for the proposed approach in both convex and non-convex settings. We then experimentally demonstrate that our algorithms outperform the competitor methods by achieving faster convergence and recovering better quality and flatter local optima. We also carry out an ablation study to analyze the scalability of the proposed algorithms in more crowded distributed training environments. Finally, we report that our approach requires less frequent communication and fewer distributed updates compared to the state-of-the-art baselines.

TAME: Task Agnostic Continual Learning using Multiple Experts

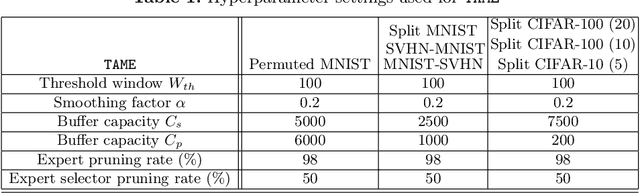
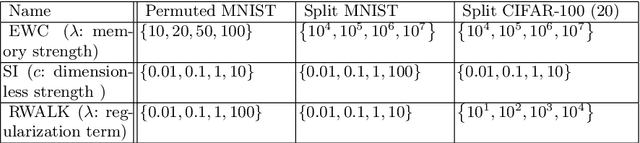
The goal of lifelong learning is to continuously learn from non-stationary distributions, where the non-stationarity is typically imposed by a sequence of distinct tasks. Prior works have mostly considered idealistic settings, where the identity of tasks is known at least at training. In this paper we focus on a fundamentally harder, so-called task-agnostic setting where the task identities are not known and the learning machine needs to infer them from the observations. Our algorithm, which we call TAME (Task-Agnostic continual learning using Multiple Experts), automatically detects the shift in data distributions and switches between task expert networks in an online manner. At training, the strategy for switching between tasks hinges on an extremely simple observation that for each new coming task there occurs a statistically-significant deviation in the value of the loss function that marks the onset of this new task. At inference, the switching between experts is governed by the selector network that forwards the test sample to its relevant expert network. The selector network is trained on a small subset of data drawn uniformly at random. We control the growth of the task expert networks as well as selector network by employing online pruning. Our experimental results show the efficacy of our approach on benchmark continual learning data sets, outperforming the previous task-agnostic methods and even the techniques that admit task identities at both training and testing, while at the same time using a comparable model size.

ERASE-Net: Efficient Segmentation Networks for Automotive Radar Signals

Among various sensors for assisted and autonomous driving systems, automotive radar has been considered as a robust and low-cost solution even in adverse weather or lighting conditions. With the recent development of radar technologies and open-sourced annotated data sets, semantic segmentation with radar signals has become very promising. However, existing methods are either computationally expensive or discard significant amounts of valuable information from raw 3D radar signals by reducing them to 2D planes via averaging. In this work, we introduce ERASE-Net, an Efficient RAdar SEgmentation Network to segment the raw radar signals semantically. The core of our approach is the novel detect-then-segment method for raw radar signals. It first detects the center point of each object, then extracts a compact radar signal representation, and finally performs semantic segmentation. We show that our method can achieve superior performance on radar semantic segmentation task compared to the state-of-the-art (SOTA) technique. Furthermore, our approach requires up to 20x less computational resources. Finally, we show that the proposed ERASE-Net can be compressed by 40% without significant loss in performance, significantly more than the SOTA network, which makes it a more promising candidate for practical automotive applications.

Low-Pass Filtering SGD for Recovering Flat Optima in the Deep Learning Optimization Landscape

In this paper, we study the sharpness of a deep learning (DL) loss landscape around local minima in order to reveal systematic mechanisms underlying the generalization abilities of DL models. Our analysis is performed across varying network and optimizer hyper-parameters, and involves a rich family of different sharpness measures. We compare these measures and show that the low-pass filter-based measure exhibits the highest correlation with the generalization abilities of DL models, has high robustness to both data and label noise, and furthermore can track the double descent behavior for neural networks. We next derive the optimization algorithm, relying on the low-pass filter (LPF), that actively searches the flat regions in the DL optimization landscape using SGD-like procedure. The update of the proposed algorithm, that we call LPF-SGD, is determined by the gradient of the convolution of the filter kernel with the loss function and can be efficiently computed using MC sampling. We empirically show that our algorithm achieves superior generalization performance compared to the common DL training strategies. On the theoretical front, we prove that LPF-SGD converges to a better optimal point with smaller generalization error than SGD.

AutoDrop: Training Deep Learning Models with Automatic Learning Rate Drop

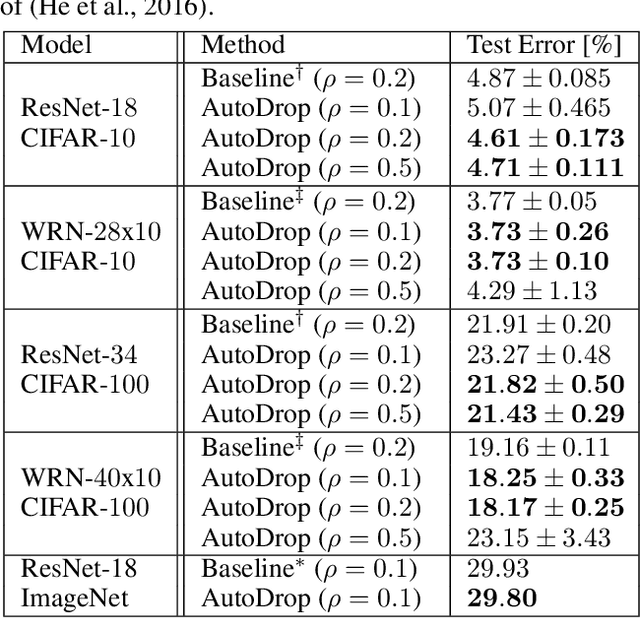
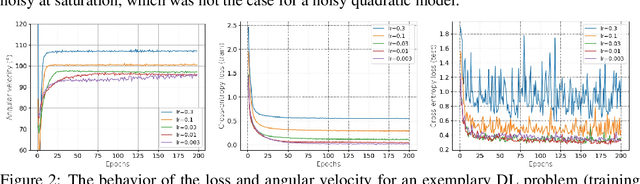
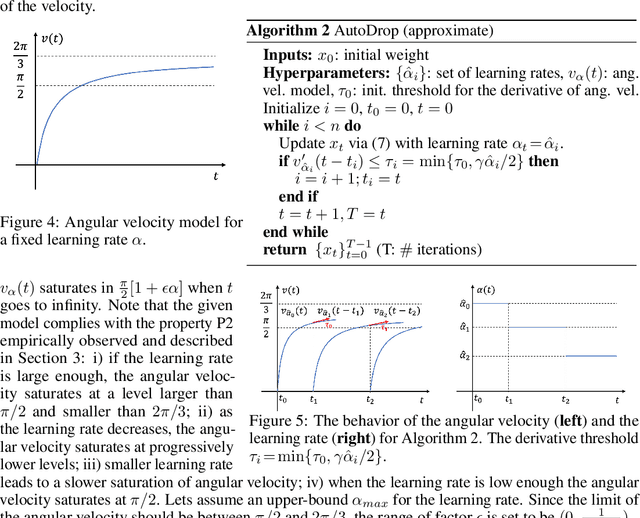
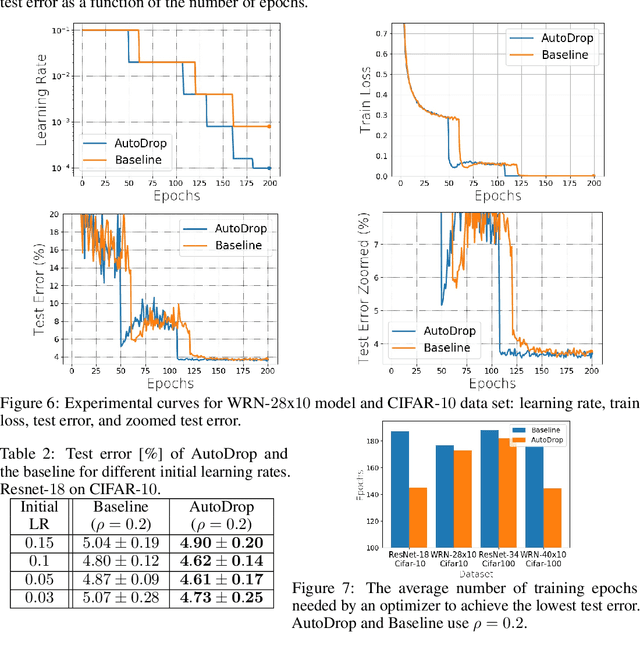
Modern deep learning (DL) architectures are trained using variants of the SGD algorithm that is run with a $\textit{manually}$ defined learning rate schedule, i.e., the learning rate is dropped at the pre-defined epochs, typically when the training loss is expected to saturate. In this paper we develop an algorithm that realizes the learning rate drop $\textit{automatically}$. The proposed method, that we refer to as AutoDrop, is motivated by the observation that the angular velocity of the model parameters, i.e., the velocity of the changes of the convergence direction, for a fixed learning rate initially increases rapidly and then progresses towards soft saturation. At saturation the optimizer slows down thus the angular velocity saturation is a good indicator for dropping the learning rate. After the drop, the angular velocity "resets" and follows the previously described pattern - it increases again until saturation. We show that our method improves over SOTA training approaches: it accelerates the training of DL models and leads to a better generalization. We also show that our method does not require any extra hyperparameter tuning. AutoDrop is furthermore extremely simple to implement and computationally cheap. Finally, we develop a theoretical framework for analyzing our algorithm and provide convergence guarantees.

A Theoretical-Empirical Approach to Estimating Sample Complexity of DNNs

This paper focuses on understanding how the generalization error scales with the amount of the training data for deep neural networks (DNNs). Existing techniques in statistical learning require computation of capacity measures, such as VC dimension, to provably bound this error. It is however unclear how to extend these measures to DNNs and therefore the existing analyses are applicable to simple neural networks, which are not used in practice, e.g., linear or shallow ones or otherwise multi-layer perceptrons. Moreover, many theoretical error bounds are not empirically verifiable. We derive estimates of the generalization error that hold for deep networks and do not rely on unattainable capacity measures. The enabling technique in our approach hinges on two major assumptions: i) the network achieves zero training error, ii) the probability of making an error on a test point is proportional to the distance between this point and its nearest training point in the feature space and at a certain maximal distance (that we call radius) it saturates. Based on these assumptions we estimate the generalization error of DNNs. The obtained estimate scales as O(1/(\delta N^{1/d})), where N is the size of the training data and is parameterized by two quantities, the effective dimensionality of the data as perceived by the network (d) and the aforementioned radius (\delta), both of which we find empirically. We show that our estimates match with the experimentally obtained behavior of the error on multiple learning tasks using benchmark data-sets and realistic models. Estimating training data requirements is essential for deployment of safety critical applications such as autonomous driving etc. Furthermore, collecting and annotating training data requires a huge amount of financial, computational and human resources. Our empirical estimates will help to efficiently allocate resources.

Backdoor Attacks on the DNN Interpretation System

Interpretability is crucial to understand the inner workings of deep neural networks (DNNs) and many interpretation methods generate saliency maps that highlight parts of the input image that contribute the most to the prediction made by the DNN. In this paper we design a backdoor attack that alters the saliency map produced by the network for an input image only with injected trigger that is invisible to the naked eye while maintaining the prediction accuracy. The attack relies on injecting poisoned data with a trigger into the training data set. The saliency maps are incorporated in the penalty term of the objective function that is used to train a deep model and its influence on model training is conditioned upon the presence of a trigger. We design two types of attacks: targeted attack that enforces a specific modification of the saliency map and untargeted attack when the importance scores of the top pixels from the original saliency map are significantly reduced. We perform empirical evaluation of the proposed backdoor attacks on gradient-based and gradient-free interpretation methods for a variety of deep learning architectures. We show that our attacks constitute a serious security threat when deploying deep learning models developed by untrusty sources. Finally, in the Supplement we demonstrate that the proposed methodology can be used in an inverted setting, where the correct saliency map can be obtained only in the presence of a trigger (key), effectively making the interpretation system available only to selected users.