A Theoretical-Empirical Approach to Estimating Sample Complexity of DNNs

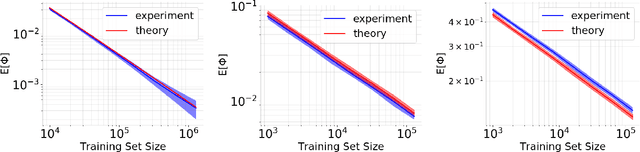
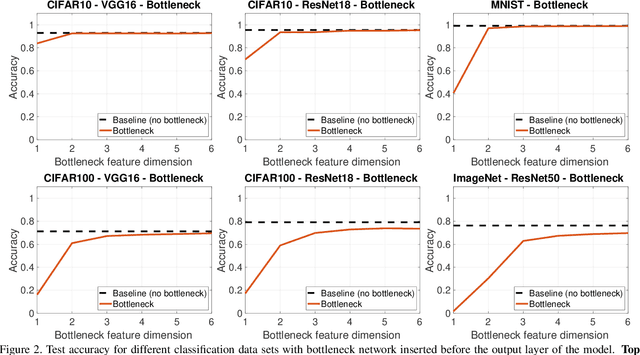
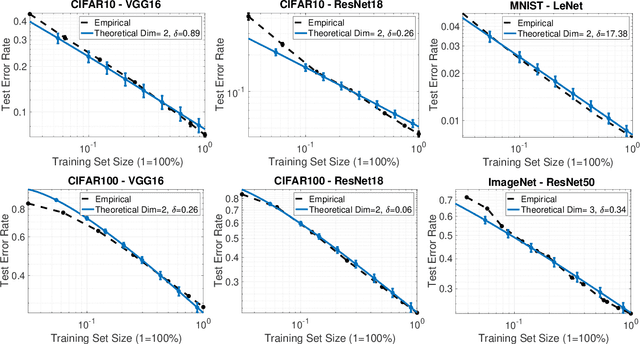
This paper focuses on understanding how the generalization error scales with the amount of the training data for deep neural networks (DNNs). Existing techniques in statistical learning require computation of capacity measures, such as VC dimension, to provably bound this error. It is however unclear how to extend these measures to DNNs and therefore the existing analyses are applicable to simple neural networks, which are not used in practice, e.g., linear or shallow ones or otherwise multi-layer perceptrons. Moreover, many theoretical error bounds are not empirically verifiable. We derive estimates of the generalization error that hold for deep networks and do not rely on unattainable capacity measures. The enabling technique in our approach hinges on two major assumptions: i) the network achieves zero training error, ii) the probability of making an error on a test point is proportional to the distance between this point and its nearest training point in the feature space and at a certain maximal distance (that we call radius) it saturates. Based on these assumptions we estimate the generalization error of DNNs. The obtained estimate scales as O(1/(\delta N^{1/d})), where N is the size of the training data and is parameterized by two quantities, the effective dimensionality of the data as perceived by the network (d) and the aforementioned radius (\delta), both of which we find empirically. We show that our estimates match with the experimentally obtained behavior of the error on multiple learning tasks using benchmark data-sets and realistic models. Estimating training data requirements is essential for deployment of safety critical applications such as autonomous driving etc. Furthermore, collecting and annotating training data requires a huge amount of financial, computational and human resources. Our empirical estimates will help to efficiently allocate resources.