Federated learning with incremental clustering for heterogeneous data

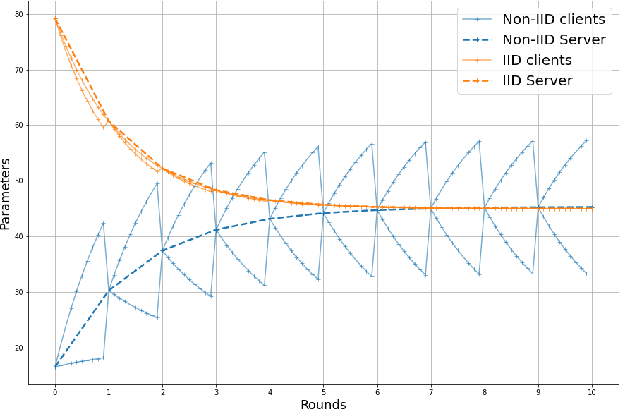
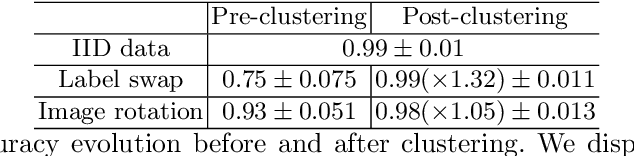
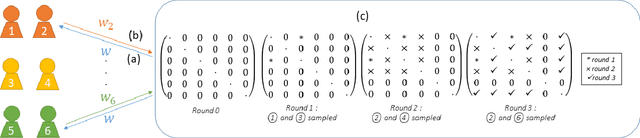
Federated learning enables different parties to collaboratively build a global model under the orchestration of a server while keeping the training data on clients' devices. However, performance is affected when clients have heterogeneous data. To cope with this problem, we assume that despite data heterogeneity, there are groups of clients who have similar data distributions that can be clustered. In previous approaches, in order to cluster clients the server requires clients to send their parameters simultaneously. However, this can be problematic in a context where there is a significant number of participants that may have limited availability. To prevent such a bottleneck, we propose FLIC (Federated Learning with Incremental Clustering), in which the server exploits the updates sent by clients during federated training instead of asking them to send their parameters simultaneously. Hence no additional communications between the server and the clients are necessary other than what classical federated learning requires. We empirically demonstrate for various non-IID cases that our approach successfully splits clients into groups following the same data distributions. We also identify the limitations of FLIC by studying its capability to partition clients at the early stages of the federated learning process efficiently. We further address attacks on models as a form of data heterogeneity and empirically show that FLIC is a robust defense against poisoning attacks even when the proportion of malicious clients is higher than 50\%.

Structured adaptive and random spinners for fast machine learning computations

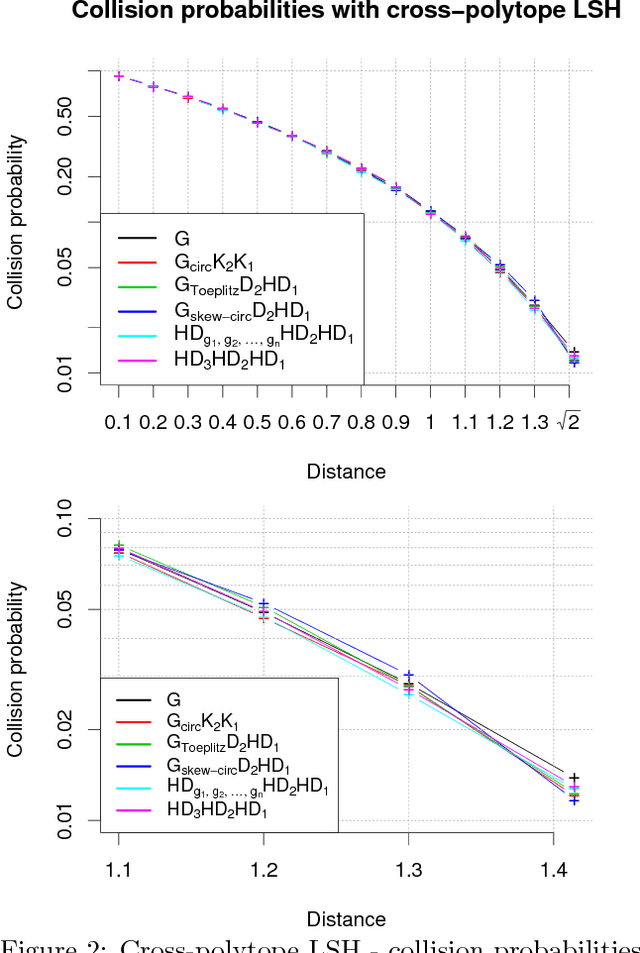
We consider an efficient computational framework for speeding up several machine learning algorithms with almost no loss of accuracy. The proposed framework relies on projections via structured matrices that we call Structured Spinners, which are formed as products of three structured matrix-blocks that incorporate rotations. The approach is highly generic, i.e. i) structured matrices under consideration can either be fully-randomized or learned, ii) our structured family contains as special cases all previously considered structured schemes, iii) the setting extends to the non-linear case where the projections are followed by non-linear functions, and iv) the method finds numerous applications including kernel approximations via random feature maps, dimensionality reduction algorithms, new fast cross-polytope LSH techniques, deep learning, convex optimization algorithms via Newton sketches, quantization with random projection trees, and more. The proposed framework comes with theoretical guarantees characterizing the capacity of the structured model in reference to its unstructured counterpart and is based on a general theoretical principle that we describe in the paper. As a consequence of our theoretical analysis, we provide the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the HD3HD2HD1 structured matrix [Andoni et al., 2015]. The exhaustive experimental evaluation confirms the accuracy and efficiency of structured spinners for a variety of different applications.

TripleSpin - a generic compact paradigm for fast machine learning computations

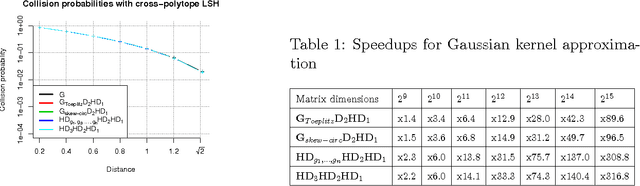
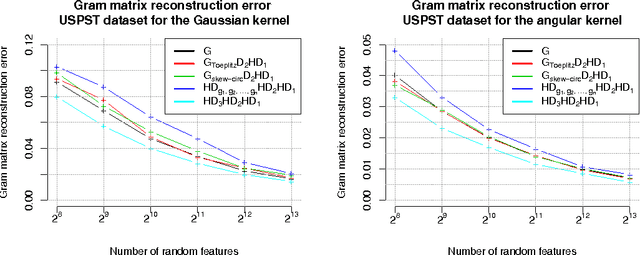
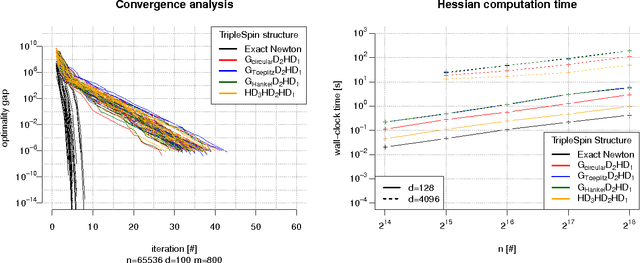
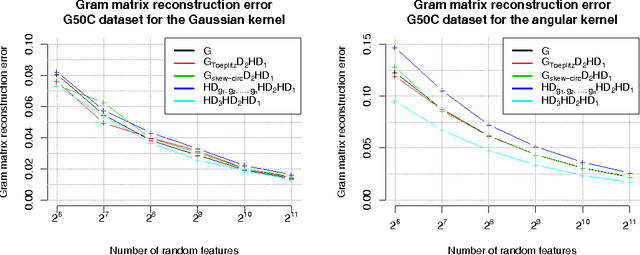
We present a generic compact computational framework relying on structured random matrices that can be applied to speed up several machine learning algorithms with almost no loss of accuracy. The applications include new fast LSH-based algorithms, efficient kernel computations via random feature maps, convex optimization algorithms, quantization techniques and many more. Certain models of the presented paradigm are even more compressible since they apply only bit matrices. This makes them suitable for deploying on mobile devices. All our findings come with strong theoretical guarantees. In particular, as a byproduct of the presented techniques and by using relatively new Berry-Esseen-type CLT for random vectors, we give the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the $\textbf{HD}_{3}\textbf{HD}_{2}\textbf{HD}_{1}$ structured matrix ("Practical and Optimal LSH for Angular Distance"). These guarantees as well as theoretical results for other aforementioned applications follow from the same general theoretical principle that we present in the paper. Our structured family contains as special cases all previously considered structured schemes, including the recently introduced $P$-model. Experimental evaluation confirms the accuracy and efficiency of TripleSpin matrices.