Self-supervised object detection from audio-visual correspondence

We tackle the problem of learning object detectors without supervision. Differently from weakly-supervised object detection, we do not assume image-level class labels. Instead, we extract a supervisory signal from audio-visual data, using the audio component to "teach" the object detector. While this problem is related to sound source localisation, it is considerably harder because the detector must classify the objects by type, enumerate each instance of the object, and do so even when the object is silent. We tackle this problem by first designing a self-supervised framework with a contrastive objective that jointly learns to classify and localise objects. Then, without using any supervision, we simply use these self-supervised labels and boxes to train an image-based object detector. With this, we outperform previous unsupervised and weakly-supervised detectors for the task of object detection and sound source localization. We also show that we can align this detector to ground-truth classes with as little as one label per pseudo-class, and show how our method can learn to detect generic objects that go beyond instruments, such as airplanes and cats.

Robust Implicit Backpropagation

Arguably the biggest challenge in applying neural networks is tuning the hyperparameters, in particular the learning rate. The sensitivity to the learning rate is due to the reliance on backpropagation to train the network. In this paper we present the first application of Implicit Stochastic Gradient Descent (ISGD) to train neural networks, a method known in convex optimization to be unconditionally stable and robust to the learning rate. Our key contribution is a novel layer-wise approximation of ISGD which makes its updates tractable for neural networks. Experiments show that our method is more robust to high learning rates and generally outperforms standard backpropagation on a variety of tasks.

Unbiased scalable softmax optimization

Recent neural network and language models rely on softmax distributions with an extremely large number of categories. Since calculating the softmax normalizing constant in this context is prohibitively expensive, there is a growing literature of efficiently computable but biased estimates of the softmax. In this paper we propose the first unbiased algorithms for maximizing the softmax likelihood whose work per iteration is independent of the number of classes and datapoints (and no extra work is required at the end of each epoch). We show that our proposed unbiased methods comprehensively outperform the state-of-the-art on seven real world datasets.

Structured adaptive and random spinners for fast machine learning computations

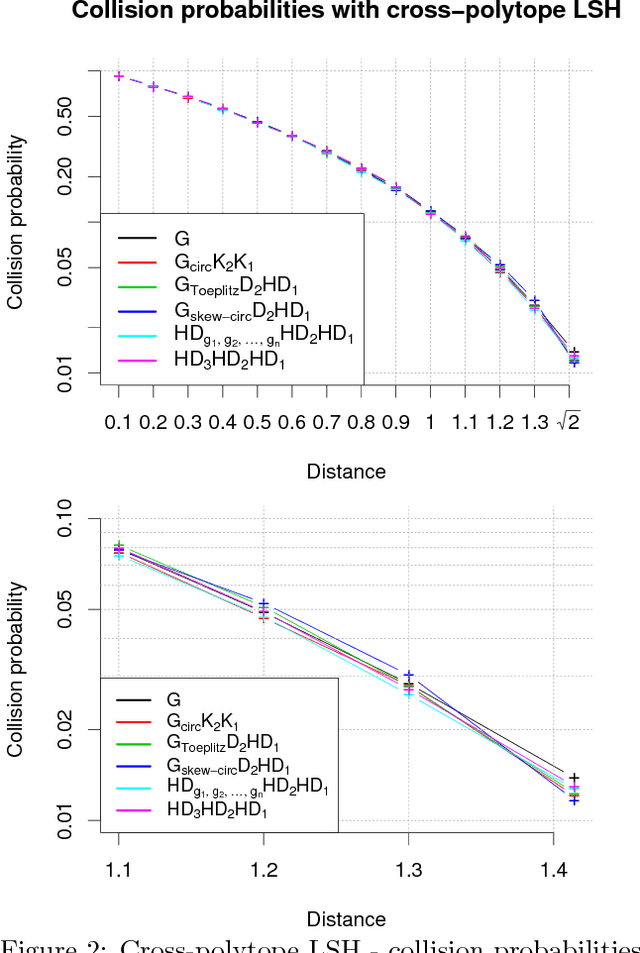
We consider an efficient computational framework for speeding up several machine learning algorithms with almost no loss of accuracy. The proposed framework relies on projections via structured matrices that we call Structured Spinners, which are formed as products of three structured matrix-blocks that incorporate rotations. The approach is highly generic, i.e. i) structured matrices under consideration can either be fully-randomized or learned, ii) our structured family contains as special cases all previously considered structured schemes, iii) the setting extends to the non-linear case where the projections are followed by non-linear functions, and iv) the method finds numerous applications including kernel approximations via random feature maps, dimensionality reduction algorithms, new fast cross-polytope LSH techniques, deep learning, convex optimization algorithms via Newton sketches, quantization with random projection trees, and more. The proposed framework comes with theoretical guarantees characterizing the capacity of the structured model in reference to its unstructured counterpart and is based on a general theoretical principle that we describe in the paper. As a consequence of our theoretical analysis, we provide the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the HD3HD2HD1 structured matrix [Andoni et al., 2015]. The exhaustive experimental evaluation confirms the accuracy and efficiency of structured spinners for a variety of different applications.

TripleSpin - a generic compact paradigm for fast machine learning computations

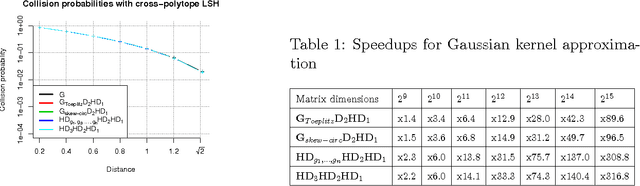
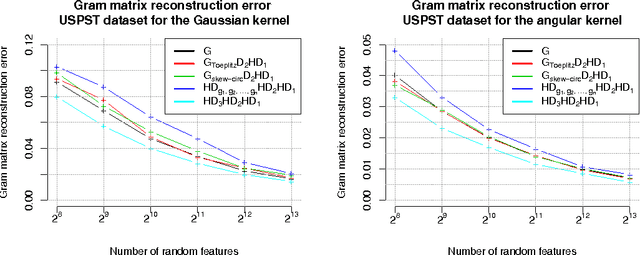
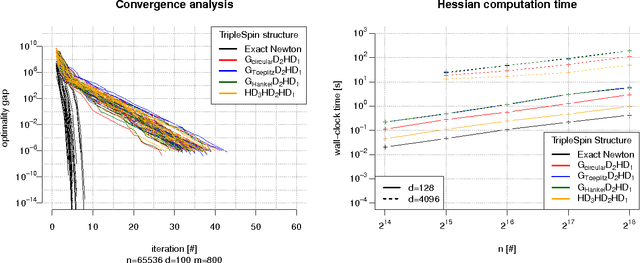
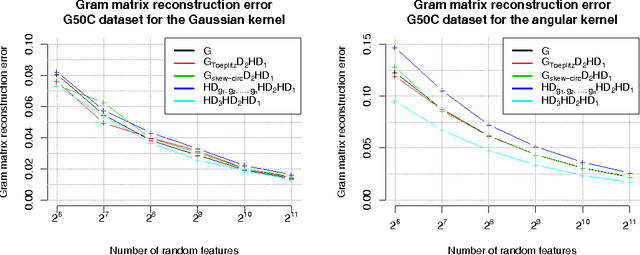
We present a generic compact computational framework relying on structured random matrices that can be applied to speed up several machine learning algorithms with almost no loss of accuracy. The applications include new fast LSH-based algorithms, efficient kernel computations via random feature maps, convex optimization algorithms, quantization techniques and many more. Certain models of the presented paradigm are even more compressible since they apply only bit matrices. This makes them suitable for deploying on mobile devices. All our findings come with strong theoretical guarantees. In particular, as a byproduct of the presented techniques and by using relatively new Berry-Esseen-type CLT for random vectors, we give the first theoretical guarantees for one of the most efficient existing LSH algorithms based on the $\textbf{HD}_{3}\textbf{HD}_{2}\textbf{HD}_{1}$ structured matrix ("Practical and Optimal LSH for Angular Distance"). These guarantees as well as theoretical results for other aforementioned applications follow from the same general theoretical principle that we present in the paper. Our structured family contains as special cases all previously considered structured schemes, including the recently introduced $P$-model. Experimental evaluation confirms the accuracy and efficiency of TripleSpin matrices.

Fast nonlinear embeddings via structured matrices

We present a new paradigm for speeding up randomized computations of several frequently used functions in machine learning. In particular, our paradigm can be applied for improving computations of kernels based on random embeddings. Above that, the presented framework covers multivariate randomized functions. As a byproduct, we propose an algorithmic approach that also leads to a significant reduction of space complexity. Our method is based on careful recycling of Gaussian vectors into structured matrices that share properties of fully random matrices. The quality of the proposed structured approach follows from combinatorial properties of the graphs encoding correlations between rows of these structured matrices. Our framework covers as special cases already known structured approaches such as the Fast Johnson-Lindenstrauss Transform, but is much more general since it can be applied also to highly nonlinear embeddings. We provide strong concentration results showing the quality of the presented paradigm.