KD$^{2}$M: An unifying framework for feature knowledge distillation

Knowledge Distillation (KD) seeks to transfer the knowledge of a teacher, towards a student neural net. This process is often done by matching the networks' predictions (i.e., their output), but, recently several works have proposed to match the distributions of neural nets' activations (i.e., their features), a process known as \emph{distribution matching}. In this paper, we propose an unifying framework, Knowledge Distillation through Distribution Matching (KD$^{2}$M), which formalizes this strategy. Our contributions are threefold. We i) provide an overview of distribution metrics used in distribution matching, ii) benchmark on computer vision datasets, and iii) derive new theoretical results for KD.

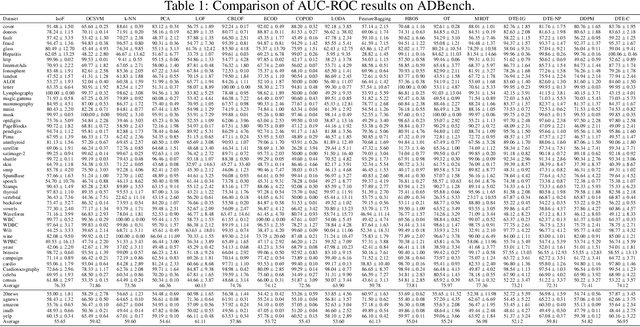
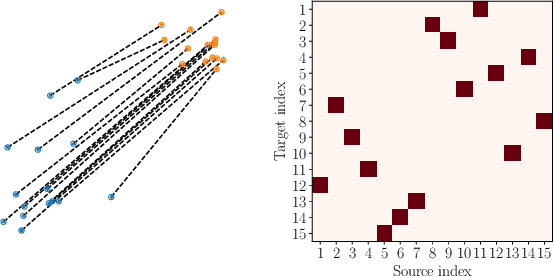
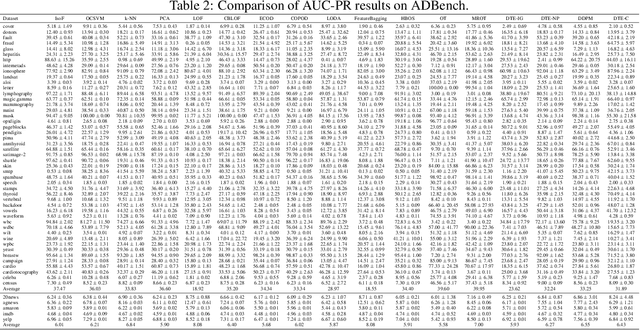
Unsupervised Anomaly Detection through Mass Repulsing Optimal Transport

Detecting anomalies in datasets is a longstanding problem in machine learning. In this context, anomalies are defined as a sample that significantly deviates from the remaining data. Meanwhile, optimal transport (OT) is a field of mathematics concerned with the transportation, between two probability measures, at least effort. In classical OT, the optimal transportation strategy of a measure to itself is the identity. In this paper, we tackle anomaly detection by forcing samples to displace its mass, while keeping the least effort objective. We call this new transportation problem Mass Repulsing Optimal Transport (MROT). Naturally, samples lying in low density regions of space will be forced to displace mass very far, incurring a higher transportation cost. We use these concepts to design a new anomaly score. Through a series of experiments in existing benchmarks, and fault detection problems, we show that our algorithm improves over existing methods.

A dimensionality reduction technique based on the Gromov-Wasserstein distance

Analyzing relationships between objects is a pivotal problem within data science. In this context, Dimensionality reduction (DR) techniques are employed to generate smaller and more manageable data representations. This paper proposes a new method for dimensionality reduction, based on optimal transportation theory and the Gromov-Wasserstein distance. We offer a new probabilistic view of the classical Multidimensional Scaling (MDS) algorithm and the nonlinear dimensionality reduction algorithm, Isomap (Isometric Mapping or Isometric Feature Mapping) that extends the classical MDS, in which we use the Gromov-Wasserstein distance between the probability measure of high-dimensional data, and its low-dimensional representation. Through gradient descent, our method embeds high-dimensional data into a lower-dimensional space, providing a robust and efficient solution for analyzing complex high-dimensional datasets.

Online Multi-Source Domain Adaptation through Gaussian Mixtures and Dataset Dictionary Learning

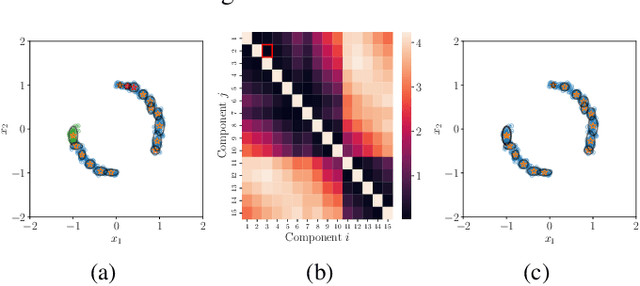
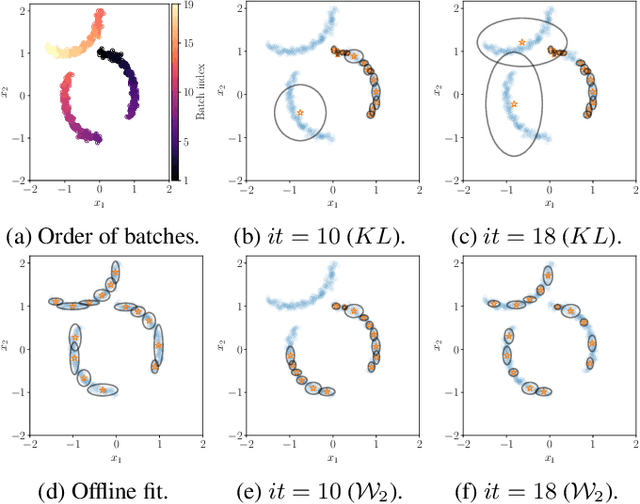
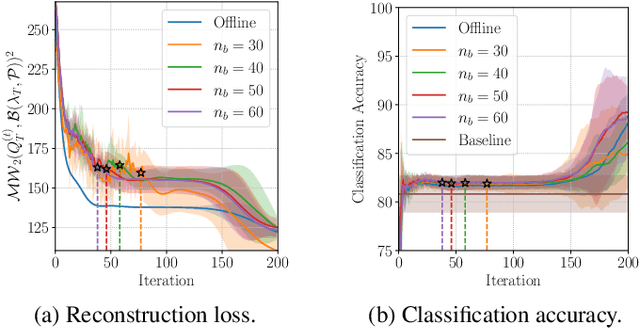
This paper addresses the challenge of online multi-source domain adaptation (MSDA) in transfer learning, a scenario where one needs to adapt multiple, heterogeneous source domains towards a target domain that comes in a stream. We introduce a novel approach for the online fit of a Gaussian Mixture Model (GMM), based on the Wasserstein geometry of Gaussian measures. We build upon this method and recent developments in dataset dictionary learning for proposing a novel strategy in online MSDA. Experiments on the challenging Tennessee Eastman Process benchmark demonstrate that our approach is able to adapt \emph{on the fly} to the stream of target domain data. Furthermore, our online GMM serves as a memory, representing the whole stream of data.

Dataset Dictionary Learning in a Wasserstein Space for Federated Domain Adaptation

Multi-Source Domain Adaptation (MSDA) is a challenging scenario where multiple related and heterogeneous source datasets must be adapted to an unlabeled target dataset. Conventional MSDA methods often overlook that data holders may have privacy concerns, hindering direct data sharing. In response, decentralized MSDA has emerged as a promising strategy to achieve adaptation without centralizing clients' data. Our work proposes a novel approach, Decentralized Dataset Dictionary Learning, to address this challenge. Our method leverages Wasserstein barycenters to model the distributional shift across multiple clients, enabling effective adaptation while preserving data privacy. Specifically, our algorithm expresses each client's underlying distribution as a Wasserstein barycenter of public atoms, weighted by private barycentric coordinates. Our approach ensures that the barycentric coordinates remain undisclosed throughout the adaptation process. Extensive experimentation across five visual domain adaptation benchmarks demonstrates the superiority of our strategy over existing decentralized MSDA techniques. Moreover, our method exhibits enhanced robustness to client parallelism while maintaining relative resilience compared to conventional decentralized MSDA methodologies.

Lighter, Better, Faster Multi-Source Domain Adaptation with Gaussian Mixture Models and Optimal Transport

In this paper, we tackle Multi-Source Domain Adaptation (MSDA), a task in transfer learning where one adapts multiple heterogeneous, labeled source probability measures towards a different, unlabeled target measure. We propose a novel framework for MSDA, based on Optimal Transport (OT) and Gaussian Mixture Models (GMMs). Our framework has two key advantages. First, OT between GMMs can be solved efficiently via linear programming. Second, it provides a convenient model for supervised learning, especially classification, as components in the GMM can be associated with existing classes. Based on the GMM-OT problem, we propose a novel technique for calculating barycenters of GMMs. Based on this novel algorithm, we propose two new strategies for MSDA: GMM-WBT and GMM-DaDiL. We empirically evaluate our proposed methods on four benchmarks in image classification and fault diagnosis, showing that we improve over the prior art while being faster and involving fewer parameters.

Optimal Transport for Domain Adaptation through Gaussian Mixture Models

In this paper we explore domain adaptation through optimal transport. We propose a novel approach, where we model the data distributions through Gaussian mixture models. This strategy allows us to solve continuous optimal transport through an equivalent discrete problem. The optimal transport solution gives us a matching between source and target domain mixture components. From this matching, we can map data points between domains, or transfer the labels from the source domain components towards the target domain. We experiment with 2 domain adaptation benchmarks in fault diagnosis, showing that our methods have state-of-the-art performance.

Multi-Source Domain Adaptation meets Dataset Distillation through Dataset Dictionary Learning

In this paper, we consider the intersection of two problems in machine learning: Multi-Source Domain Adaptation (MSDA) and Dataset Distillation (DD). On the one hand, the first considers adapting multiple heterogeneous labeled source domains to an unlabeled target domain. On the other hand, the second attacks the problem of synthesizing a small summary containing all the information about the datasets. We thus consider a new problem called MSDA-DD. To solve it, we adapt previous works in the MSDA literature, such as Wasserstein Barycenter Transport and Dataset Dictionary Learning, as well as DD method Distribution Matching. We thoroughly experiment with this novel problem on four benchmarks (Caltech-Office 10, Tennessee-Eastman Process, Continuous Stirred Tank Reactor, and Case Western Reserve University), where we show that, even with as little as 1 sample per class, one achieves state-of-the-art adaptation performance.

Federated Dataset Dictionary Learning for Multi-Source Domain Adaptation

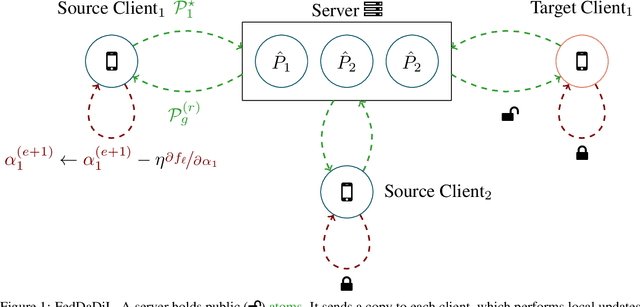
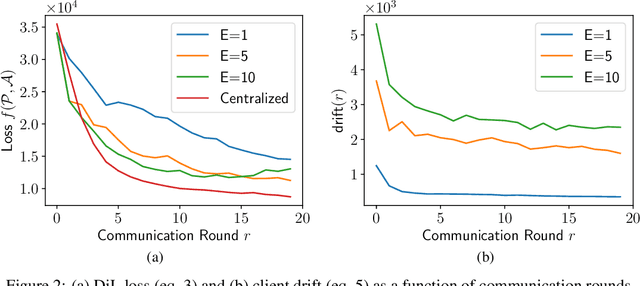
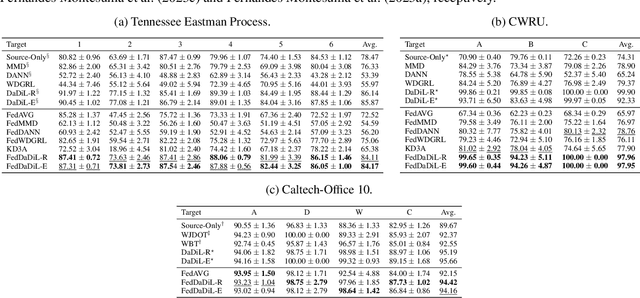
In this article, we propose an approach for federated domain adaptation, a setting where distributional shift exists among clients and some have unlabeled data. The proposed framework, FedDaDiL, tackles the resulting challenge through dictionary learning of empirical distributions. In our setting, clients' distributions represent particular domains, and FedDaDiL collectively trains a federated dictionary of empirical distributions. In particular, we build upon the Dataset Dictionary Learning framework by designing collaborative communication protocols and aggregation operations. The chosen protocols keep clients' data private, thus enhancing overall privacy compared to its centralized counterpart. We empirically demonstrate that our approach successfully generates labeled data on the target domain with extensive experiments on (i) Caltech-Office, (ii) TEP, and (iii) CWRU benchmarks. Furthermore, we compare our method to its centralized counterpart and other benchmarks in federated domain adaptation.

Multi-Source Domain Adaptation for Cross-Domain Fault Diagnosis of Chemical Processes

Fault diagnosis is an essential component in process supervision. Indeed, it determines which kind of fault has occurred, given that it has been previously detected, allowing for appropriate intervention. Automatic fault diagnosis systems use machine learning for predicting the fault type from sensor readings. Nonetheless, these models are sensible to changes in the data distributions, which may be caused by changes in the monitored process, such as changes in the mode of operation. This scenario is known as Cross-Domain Fault Diagnosis (CDFD). We provide an extensive comparison of single and multi-source unsupervised domain adaptation (SSDA and MSDA respectively) algorithms for CDFD. We study these methods in the context of the Tennessee-Eastmann Process, a widely used benchmark in the chemical industry. We show that using multiple domains during training has a positive effect, even when no adaptation is employed. As such, the MSDA baseline improves over the SSDA baseline classification accuracy by 23% on average. In addition, under the multiple-sources scenario, we improve classification accuracy of the no adaptation setting by 8.4% on average.