Optimal Transport for Domain Adaptation through Gaussian Mixture Models

In this paper we explore domain adaptation through optimal transport. We propose a novel approach, where we model the data distributions through Gaussian mixture models. This strategy allows us to solve continuous optimal transport through an equivalent discrete problem. The optimal transport solution gives us a matching between source and target domain mixture components. From this matching, we can map data points between domains, or transfer the labels from the source domain components towards the target domain. We experiment with 2 domain adaptation benchmarks in fault diagnosis, showing that our methods have state-of-the-art performance.

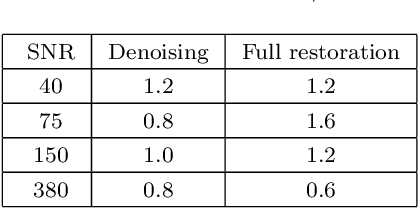
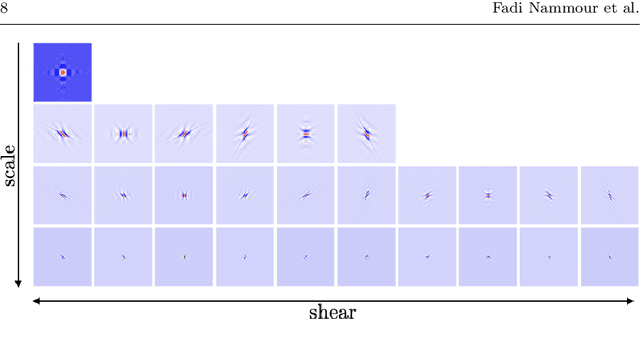
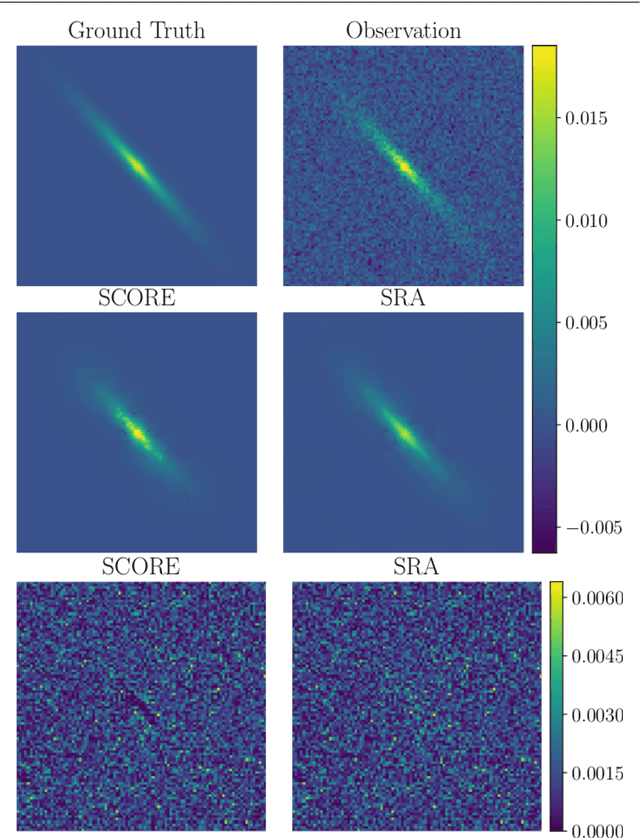
Galaxy Image Restoration with Shape Constraint

Images acquired with a telescope are blurred and corrupted by noise. The blurring is usually modeled by a convolution with the Point Spread Function and the noise by Additive Gaussian Noise. Recovering the observed image is an ill-posed inverse problem. Sparse deconvolution is well known to be an efficient deconvolution technique, leading to optimized pixel Mean Square Errors, but without any guarantee that the shapes of objects (e.g. galaxy images) contained in the data will be preserved. In this paper, we introduce a new shape constraint and exhibit its properties. By combining it with a standard sparse regularization in the wavelet domain, we introduce the Shape COnstraint REstoration algorithm (SCORE), which performs a standard sparse deconvolution, while preserving galaxy shapes. We show through numerical experiments that this new approach leads to a reduction of galaxy ellipticity measurement errors by at least 44%.

Wasserstein Dictionary Learning: Optimal Transport-based unsupervised non-linear dictionary learning

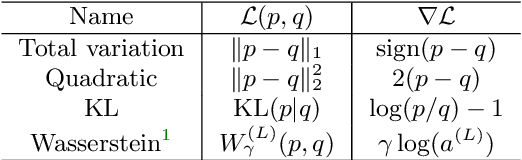
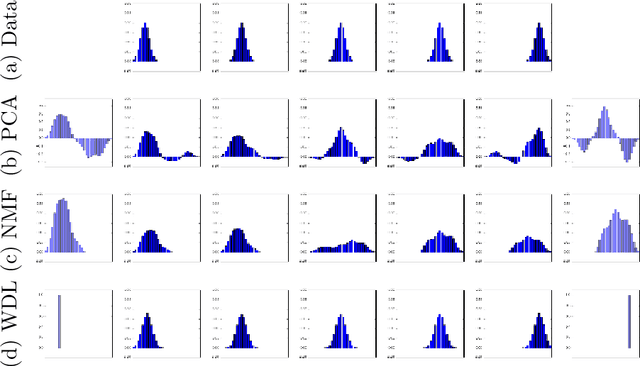
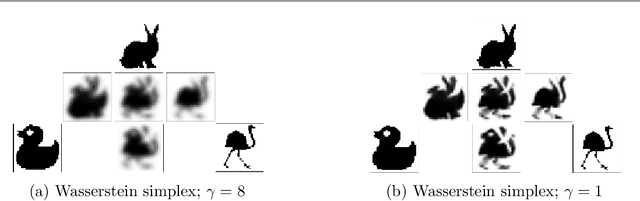
This paper introduces a new nonlinear dictionary learning method for histograms in the probability simplex. The method leverages optimal transport theory, in the sense that our aim is to reconstruct histograms using so-called displacement interpolations (a.k.a. Wasserstein barycenters) between dictionary atoms; such atoms are themselves synthetic histograms in the probability simplex. Our method simultaneously estimates such atoms, and, for each datapoint, the vector of weights that can optimally reconstruct it as an optimal transport barycenter of such atoms. Our method is computationally tractable thanks to the addition of an entropic regularization to the usual optimal transportation problem, leading to an approximation scheme that is efficient, parallel and simple to differentiate. Both atoms and weights are learned using a gradient-based descent method. Gradients are obtained by automatic differentiation of the generalized Sinkhorn iterations that yield barycenters with entropic smoothing. Because of its formulation relying on Wasserstein barycenters instead of the usual matrix product between dictionary and codes, our method allows for nonlinear relationships between atoms and the reconstruction of input data. We illustrate its application in several different image processing settings.

Super-resolution method using sparse regularization for point-spread function recovery

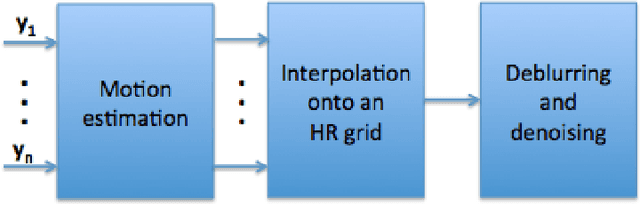
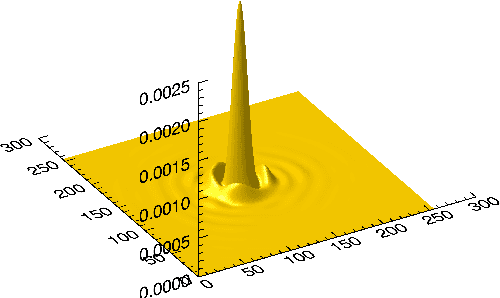
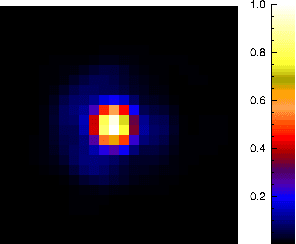
In large-scale spatial surveys, such as the forthcoming ESA Euclid mission, images may be undersampled due to the optical sensors sizes. Therefore, one may consider using a super-resolution (SR) method to recover aliased frequencies, prior to further analysis. This is particularly relevant for point-source images, which provide direct measurements of the instrument point-spread function (PSF). We introduce SPRITE, SParse Recovery of InsTrumental rEsponse, which is an SR algorithm using a sparse analysis prior. We show that such a prior provides significant improvements over existing methods, especially on low SNR PSFs.