Deep learning-based deconvolution for interferometric radio transient reconstruction

Radio astronomy is currently thriving with new large ground-based radio telescopes coming online in preparation for the upcoming Square Kilometre Array (SKA). Facilities like LOFAR, MeerKAT/SKA, ASKAP/SKA, and the future SKA-LOW bring tremendous sensitivity in time and frequency, improved angular resolution, and also high-rate data streams that need to be processed. They enable advanced studies of radio transients, volatile by nature, that can be detected or missed in the data. These transients are markers of high-energy accelerations of electrons and manifest in a wide range of temporal scales. Usually studied with dynamic spectroscopy of time series analysis, there is a motivation to search for such sources in large interferometric datasets. This requires efficient and robust signal reconstruction algorithms. To correctly account for the temporal dependency of the data, we improve the classical image deconvolution inverse problem by adding the temporal dependency in the reconstruction problem. Then, we introduce two novel neural network architectures that can do both spatial and temporal modeling of the data and the instrumental response. Then, we simulate representative time-dependent image cubes of point source distributions and realistic telescope pointings of MeerKAT to generate toy models to build the training, validation, and test datasets. Finally, based on the test data, we evaluate the source profile reconstruction performance of the proposed methods and classical image deconvolution algorithm CLEAN applied frame-by-frame. In the presence of increasing noise level in data frame, the proposed methods display a high level of robustness compared to frame-by-frame imaging with CLEAN. The deconvolved image cubes bring a factor of 3 improvement in fidelity of the recovered temporal profiles and a factor of 2 improvement in background denoising.

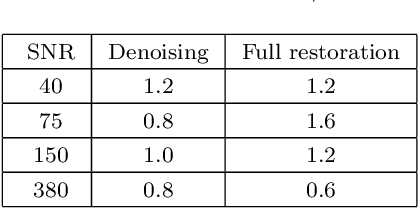
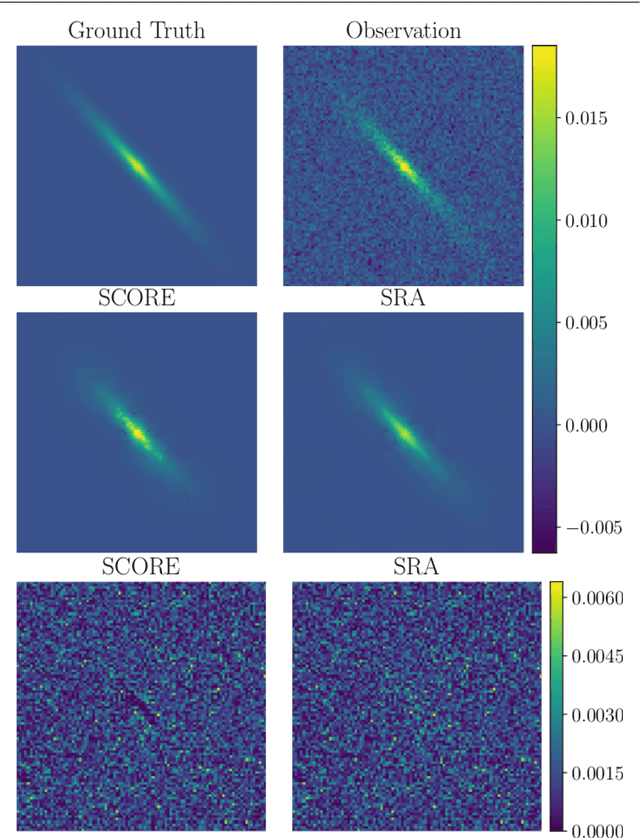
Galaxy Image Restoration with Shape Constraint

Images acquired with a telescope are blurred and corrupted by noise. The blurring is usually modeled by a convolution with the Point Spread Function and the noise by Additive Gaussian Noise. Recovering the observed image is an ill-posed inverse problem. Sparse deconvolution is well known to be an efficient deconvolution technique, leading to optimized pixel Mean Square Errors, but without any guarantee that the shapes of objects (e.g. galaxy images) contained in the data will be preserved. In this paper, we introduce a new shape constraint and exhibit its properties. By combining it with a standard sparse regularization in the wavelet domain, we introduce the Shape COnstraint REstoration algorithm (SCORE), which performs a standard sparse deconvolution, while preserving galaxy shapes. We show through numerical experiments that this new approach leads to a reduction of galaxy ellipticity measurement errors by at least 44%.