Galaxy Image Restoration with Shape Constraint
Paper and Code
Jan 25, 2021
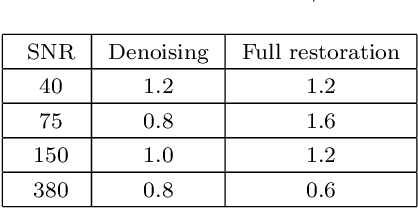
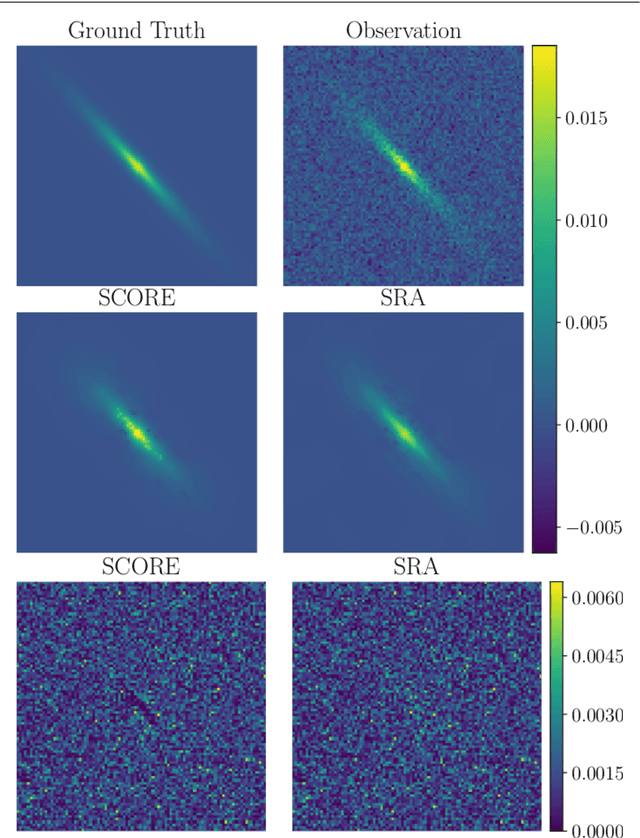
Images acquired with a telescope are blurred and corrupted by noise. The blurring is usually modeled by a convolution with the Point Spread Function and the noise by Additive Gaussian Noise. Recovering the observed image is an ill-posed inverse problem. Sparse deconvolution is well known to be an efficient deconvolution technique, leading to optimized pixel Mean Square Errors, but without any guarantee that the shapes of objects (e.g. galaxy images) contained in the data will be preserved. In this paper, we introduce a new shape constraint and exhibit its properties. By combining it with a standard sparse regularization in the wavelet domain, we introduce the Shape COnstraint REstoration algorithm (SCORE), which performs a standard sparse deconvolution, while preserving galaxy shapes. We show through numerical experiments that this new approach leads to a reduction of galaxy ellipticity measurement errors by at least 44%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge