Example-Based Sampling with Diffusion Models

Much effort has been put into developing samplers with specific properties, such as producing blue noise, low-discrepancy, lattice or Poisson disk samples. These samplers can be slow if they rely on optimization processes, may rely on a wide range of numerical methods, are not always differentiable. The success of recent diffusion models for image generation suggests that these models could be appropriate for learning how to generate point sets from examples. However, their convolutional nature makes these methods impractical for dealing with scattered data such as point sets. We propose a generic way to produce 2-d point sets imitating existing samplers from observed point sets using a diffusion model. We address the problem of convolutional layers by leveraging neighborhood information from an optimal transport matching to a uniform grid, that allows us to benefit from fast convolutions on grids, and to support the example-based learning of non-uniform sampling patterns. We demonstrate how the differentiability of our approach can be used to optimize point sets to enforce properties.

Dynamic Scene Novel View Synthesis via Deferred Spatio-temporal Consistency

Structure from motion (SfM) enables us to reconstruct a scene via casual capture from cameras at different viewpoints, and novel view synthesis (NVS) allows us to render a captured scene from a new viewpoint. Both are hard with casual capture and dynamic scenes: SfM produces noisy and spatio-temporally sparse reconstructed point clouds, resulting in NVS with spatio-temporally inconsistent effects. We consider SfM and NVS parts together to ease the challenge. First, for SfM, we recover stable camera poses, then we defer the requirement for temporally-consistent points across the scene and reconstruct only a sparse point cloud per timestep that is noisy in space-time. Second, for NVS, we present a variational diffusion formulation on depths and colors that lets us robustly cope with the noise by enforcing spatio-temporal consistency via per-pixel reprojection weights derived from the input views. Together, this deferred approach generates novel views for dynamic scenes without requiring challenging spatio-temporally consistent reconstructions nor training complex models on large datasets. We demonstrate our algorithm on real-world dynamic scenes against classic and more recent learning-based baseline approaches.

Learning to Generate Wasserstein Barycenters

Optimal transport is a notoriously difficult problem to solve numerically, with current approaches often remaining intractable for very large scale applications such as those encountered in machine learning. Wasserstein barycenters -- the problem of finding measures in-between given input measures in the optimal transport sense -- is even more computationally demanding as it requires to solve an optimization problem involving optimal transport distances. By training a deep convolutional neural network, we improve by a factor of 60 the computational speed of Wasserstein barycenters over the fastest state-of-the-art approach on the GPU, resulting in milliseconds computational times on $512\times512$ regular grids. We show that our network, trained on Wasserstein barycenters of pairs of measures, generalizes well to the problem of finding Wasserstein barycenters of more than two measures. We demonstrate the efficiency of our approach for computing barycenters of sketches and transferring colors between multiple images.

Ground Metric Learning on Graphs

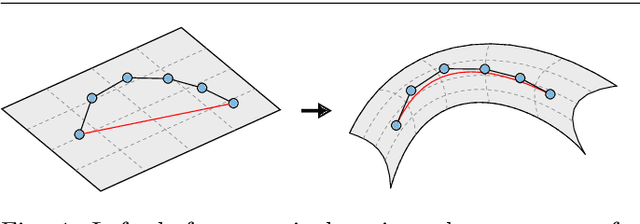
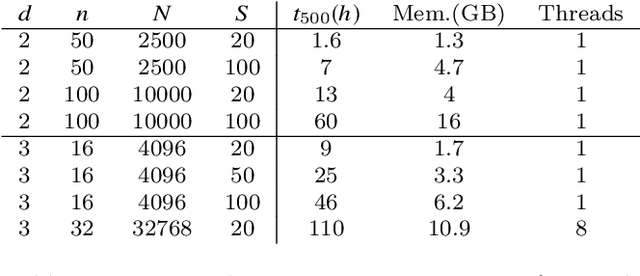
Optimal transport (OT) distances between probability distributions are parameterized by the ground metric they use between observations. Their relevance for real-life applications strongly hinges on whether that ground metric parameter is suitably chosen. Selecting it adaptively and algorithmically from prior knowledge, the so-called ground metric learning GML) problem, has therefore appeared in various settings. We consider it in this paper when the learned metric is constrained to be a geodesic distance on a graph that supports the measures of interest. This imposes a rich structure for candidate metrics, but also enables far more efficient learning procedures when compared to a direct optimization over the space of all metric matrices. We use this setting to tackle an inverse problem stemming from the observation of a density evolving with time: we seek a graph ground metric such that the OT interpolation between the starting and ending densities that result from that ground metric agrees with the observed evolution. This OT dynamic framework is relevant to model natural phenomena exhibiting displacements of mass, such as for instance the evolution of the color palette induced by the modification of lighting and materials.

Wasserstein Dictionary Learning: Optimal Transport-based unsupervised non-linear dictionary learning

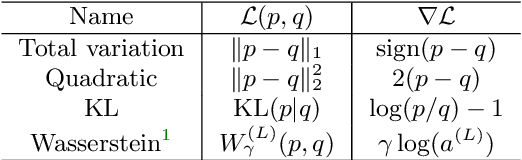
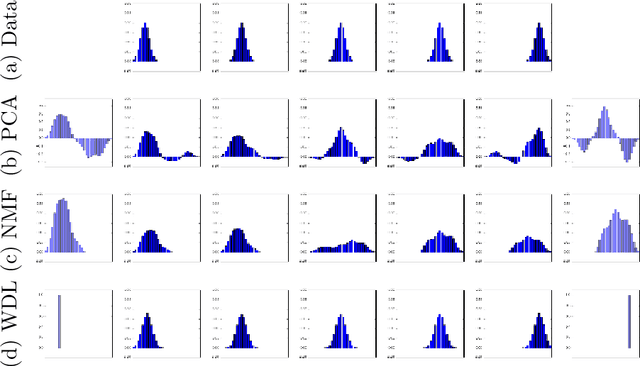
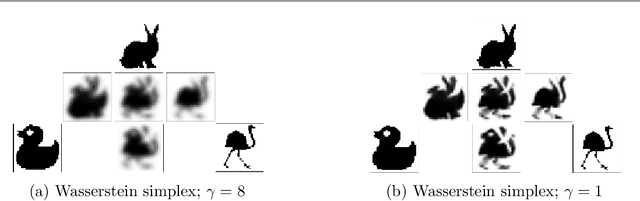
This paper introduces a new nonlinear dictionary learning method for histograms in the probability simplex. The method leverages optimal transport theory, in the sense that our aim is to reconstruct histograms using so-called displacement interpolations (a.k.a. Wasserstein barycenters) between dictionary atoms; such atoms are themselves synthetic histograms in the probability simplex. Our method simultaneously estimates such atoms, and, for each datapoint, the vector of weights that can optimally reconstruct it as an optimal transport barycenter of such atoms. Our method is computationally tractable thanks to the addition of an entropic regularization to the usual optimal transportation problem, leading to an approximation scheme that is efficient, parallel and simple to differentiate. Both atoms and weights are learned using a gradient-based descent method. Gradients are obtained by automatic differentiation of the generalized Sinkhorn iterations that yield barycenters with entropic smoothing. Because of its formulation relying on Wasserstein barycenters instead of the usual matrix product between dictionary and codes, our method allows for nonlinear relationships between atoms and the reconstruction of input data. We illustrate its application in several different image processing settings.

Efficient Decomposition of Image and Mesh Graphs by Lifted Multicuts

Formulations of the Image Decomposition Problem as a Multicut Problem (MP) w.r.t. a superpixel graph have received considerable attention. In contrast, instances of the MP w.r.t. a pixel grid graph have received little attention, firstly, because the MP is NP-hard and instances w.r.t. a pixel grid graph are hard to solve in practice, and, secondly, due to the lack of long-range terms in the objective function of the MP. We propose a generalization of the MP with long-range terms (LMP). We design and implement two efficient algorithms (primal feasible heuristics) for the MP and LMP which allow us to study instances of both problems w.r.t. the pixel grid graphs of the images in the BSDS-500 benchmark. The decompositions we obtain do not differ significantly from the state of the art, suggesting that the LMP is a competitive formulation of the Image Decomposition Problem. To demonstrate the generality of the LMP, we apply it also to the Mesh Decomposition Problem posed by the Princeton benchmark, obtaining state-of-the-art decompositions.