Example-Based Sampling with Diffusion Models

Much effort has been put into developing samplers with specific properties, such as producing blue noise, low-discrepancy, lattice or Poisson disk samples. These samplers can be slow if they rely on optimization processes, may rely on a wide range of numerical methods, are not always differentiable. The success of recent diffusion models for image generation suggests that these models could be appropriate for learning how to generate point sets from examples. However, their convolutional nature makes these methods impractical for dealing with scattered data such as point sets. We propose a generic way to produce 2-d point sets imitating existing samplers from observed point sets using a diffusion model. We address the problem of convolutional layers by leveraging neighborhood information from an optimal transport matching to a uniform grid, that allows us to benefit from fast convolutions on grids, and to support the example-based learning of non-uniform sampling patterns. We demonstrate how the differentiability of our approach can be used to optimize point sets to enforce properties.

Ground Metric Learning on Graphs

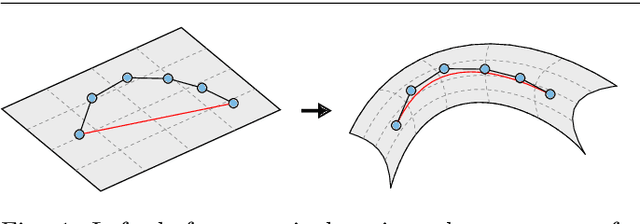
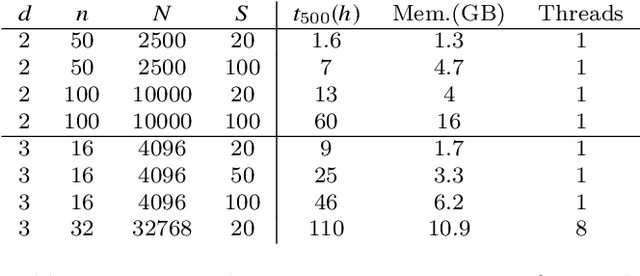
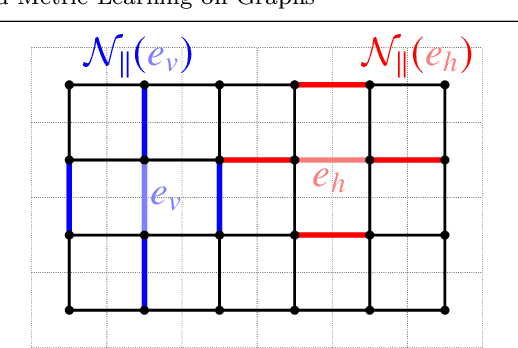
Optimal transport (OT) distances between probability distributions are parameterized by the ground metric they use between observations. Their relevance for real-life applications strongly hinges on whether that ground metric parameter is suitably chosen. Selecting it adaptively and algorithmically from prior knowledge, the so-called ground metric learning GML) problem, has therefore appeared in various settings. We consider it in this paper when the learned metric is constrained to be a geodesic distance on a graph that supports the measures of interest. This imposes a rich structure for candidate metrics, but also enables far more efficient learning procedures when compared to a direct optimization over the space of all metric matrices. We use this setting to tackle an inverse problem stemming from the observation of a density evolving with time: we seek a graph ground metric such that the OT interpolation between the starting and ending densities that result from that ground metric agrees with the observed evolution. This OT dynamic framework is relevant to model natural phenomena exhibiting displacements of mass, such as for instance the evolution of the color palette induced by the modification of lighting and materials.

Wasserstein Dictionary Learning: Optimal Transport-based unsupervised non-linear dictionary learning

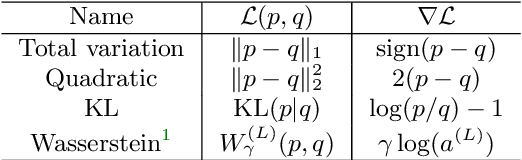
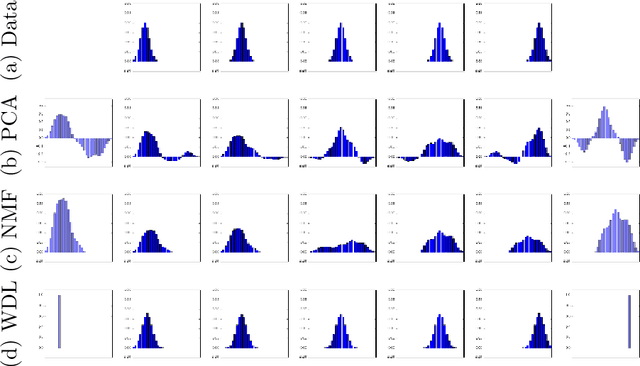
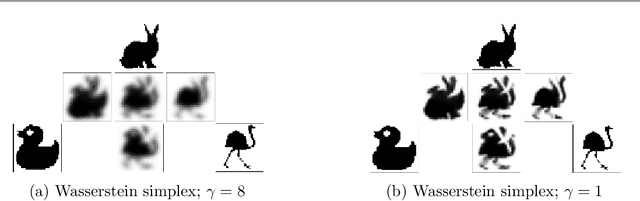
This paper introduces a new nonlinear dictionary learning method for histograms in the probability simplex. The method leverages optimal transport theory, in the sense that our aim is to reconstruct histograms using so-called displacement interpolations (a.k.a. Wasserstein barycenters) between dictionary atoms; such atoms are themselves synthetic histograms in the probability simplex. Our method simultaneously estimates such atoms, and, for each datapoint, the vector of weights that can optimally reconstruct it as an optimal transport barycenter of such atoms. Our method is computationally tractable thanks to the addition of an entropic regularization to the usual optimal transportation problem, leading to an approximation scheme that is efficient, parallel and simple to differentiate. Both atoms and weights are learned using a gradient-based descent method. Gradients are obtained by automatic differentiation of the generalized Sinkhorn iterations that yield barycenters with entropic smoothing. Because of its formulation relying on Wasserstein barycenters instead of the usual matrix product between dictionary and codes, our method allows for nonlinear relationships between atoms and the reconstruction of input data. We illustrate its application in several different image processing settings.