Top $K$ Ranking for Multi-Armed Bandit with Noisy Evaluations
Paper and Code
Dec 14, 2021
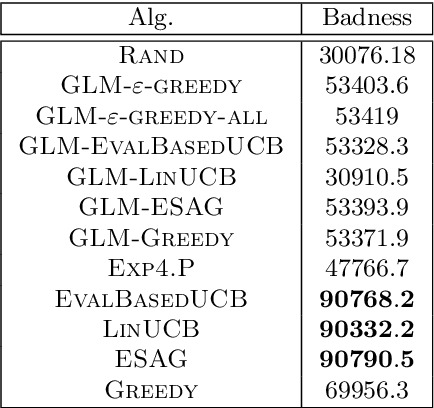
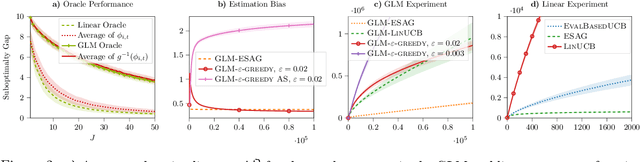
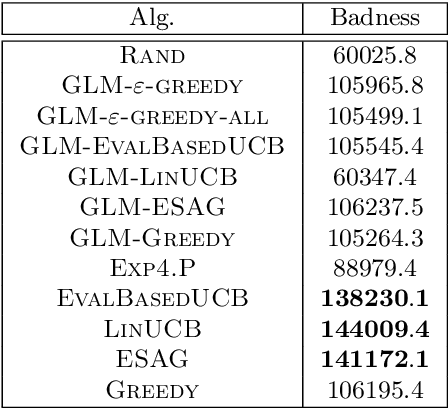
We consider a multi-armed bandit setting where, at the beginning of each round, the learner receives noisy independent, and possibly biased, \emph{evaluations} of the true reward of each arm and it selects $K$ arms with the objective of accumulating as much reward as possible over $T$ rounds. Under the assumption that at each round the true reward of each arm is drawn from a fixed distribution, we derive different algorithmic approaches and theoretical guarantees depending on how the evaluations are generated. First, we show a $\widetilde{O}(T^{2/3})$ regret in the general case when the observation functions are a genearalized linear function of the true rewards. On the other hand, we show that an improved $\widetilde{O}(\sqrt{T})$ regret can be derived when the observation functions are noisy linear functions of the true rewards. Finally, we report an empirical validation that confirms our theoretical findings, provides a thorough comparison to alternative approaches, and further supports the interest of this setting in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge