Yunchang Yang
A Reduction-based Framework for Sequential Decision Making with Delayed Feedback
Feb 06, 2023
Abstract:We study stochastic delayed feedback in general multi-agent sequential decision making, which includes bandits, single-agent Markov decision processes (MDPs), and Markov games (MGs). We propose a novel reduction-based framework, which turns any multi-batched algorithm for sequential decision making with instantaneous feedback into a sample-efficient algorithm that can handle stochastic delays in sequential decision making. By plugging different multi-batched algorithms into our framework, we provide several examples demonstrating that our framework not only matches or improves existing results for bandits, tabular MDPs, and tabular MGs, but also provides the first line of studies on delays in sequential decision making with function approximation. In summary, we provide a complete set of sharp results for multi-agent sequential decision making with delayed feedback.
Nearly Optimal Policy Optimization with Stable at Any Time Guarantee
Dec 22, 2021
Abstract:Policy optimization methods are one of the most widely used classes of Reinforcement Learning (RL) algorithms. However, theoretical understanding of these methods remains insufficient. Even in the episodic (time-inhomogeneous) tabular setting, the state-of-the-art theoretical result of policy-based method in \citet{shani2020optimistic} is only $\tilde{O}(\sqrt{S^2AH^4K})$ where $S$ is the number of states, $A$ is the number of actions, $H$ is the horizon, and $K$ is the number of episodes, and there is a $\sqrt{SH}$ gap compared with the information theoretic lower bound $\tilde{\Omega}(\sqrt{SAH^3K})$. To bridge such a gap, we propose a novel algorithm Reference-based Policy Optimization with Stable at Any Time guarantee (\algnameacro), which features the property "Stable at Any Time". We prove that our algorithm achieves $\tilde{O}(\sqrt{SAH^3K} + \sqrt{AH^4K})$ regret. When $S > H$, our algorithm is minimax optimal when ignoring logarithmic factors. To our best knowledge, RPO-SAT is the first computationally efficient, nearly minimax optimal policy-based algorithm for tabular RL.
A Unified Framework for Conservative Exploration
Jun 22, 2021
Abstract:We study bandits and reinforcement learning (RL) subject to a conservative constraint where the agent is asked to perform at least as well as a given baseline policy. This setting is particular relevant in real-world domains including digital marketing, healthcare, production, finance, etc. For multi-armed bandits, linear bandits and tabular RL, specialized algorithms and theoretical analyses were proposed in previous work. In this paper, we present a unified framework for conservative bandits and RL, in which our core technique is to calculate the necessary and sufficient budget obtained from running the baseline policy. For lower bounds, our framework gives a black-box reduction that turns a certain lower bound in the nonconservative setting into a new lower bound in the conservative setting. We strengthen the existing lower bound for conservative multi-armed bandits and obtain new lower bounds for conservative linear bandits, tabular RL and low-rank MDP. For upper bounds, our framework turns a certain nonconservative upper-confidence-bound (UCB) algorithm into a conservative algorithm with a simple analysis. For multi-armed bandits, linear bandits and tabular RL, our new upper bounds tighten or match existing ones with significantly simpler analyses. We also obtain a new upper bound for conservative low-rank MDP.
(Locally) Differentially Private Combinatorial Semi-Bandits
Jun 01, 2020
Abstract:In this paper, we study Combinatorial Semi-Bandits (CSB) that is an extension of classic Multi-Armed Bandits (MAB) under Differential Privacy (DP) and stronger Local Differential Privacy (LDP) setting. Since the server receives more information from users in CSB, it usually causes additional dependence on the dimension of data, which is a notorious side-effect for privacy preserving learning. However for CSB under two common smoothness assumptions \cite{kveton2015tight,chen2016combinatorial}, we show it is possible to remove this side-effect. In detail, for $B_{\infty}$-bounded smooth CSB under either $\varepsilon$-LDP or $\varepsilon$-DP, we prove the optimal regret bound is $\Theta(\frac{mB^2_{\infty}\ln T } {\Delta\epsilon^2})$ or $\tilde{\Theta}(\frac{mB^2_{\infty}\ln T} { \Delta\epsilon})$ respectively, where $T$ is time period, $\Delta$ is the gap of rewards and $m$ is the number of base arms, by proposing novel algorithms and matching lower bounds. For $B_1$-bounded smooth CSB under $\varepsilon$-DP, we also prove the optimal regret bound is $\tilde{\Theta}(\frac{mKB^2_1\ln T} {\Delta\epsilon})$ with both upper bound and lower bound, where $K$ is the maximum number of feedback in each round. All above results nearly match corresponding non-private optimal rates, which imply there is no additional price for (locally) differentially private CSB in above common settings.
On Layer Normalization in the Transformer Architecture
Feb 12, 2020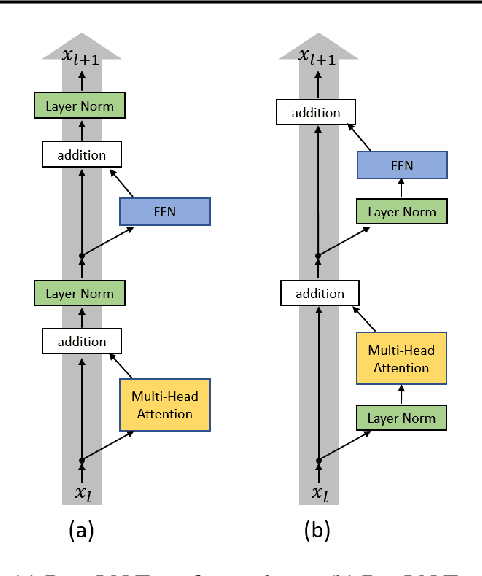

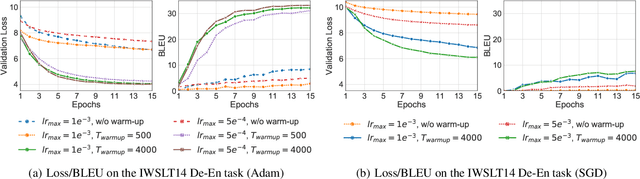

Abstract:The Transformer is widely used in natural language processing tasks. To train a Transformer however, one usually needs a carefully designed learning rate warm-up stage, which is shown to be crucial to the final performance but will slow down the optimization and bring more hyper-parameter tunings. In this paper, we first study theoretically why the learning rate warm-up stage is essential and show that the location of layer normalization matters. Specifically, we prove with mean field theory that at initialization, for the original-designed Post-LN Transformer, which places the layer normalization between the residual blocks, the expected gradients of the parameters near the output layer are large. Therefore, using a large learning rate on those gradients makes the training unstable. The warm-up stage is practically helpful for avoiding this problem. On the other hand, our theory also shows that if the layer normalization is put inside the residual blocks (recently proposed as Pre-LN Transformer), the gradients are well-behaved at initialization. This motivates us to remove the warm-up stage for the training of Pre-LN Transformers. We show in our experiments that Pre-LN Transformers without the warm-up stage can reach comparable results with baselines while requiring significantly less training time and hyper-parameter tuning on a wide range of applications.
On the Anomalous Generalization of GANs
Oct 06, 2019

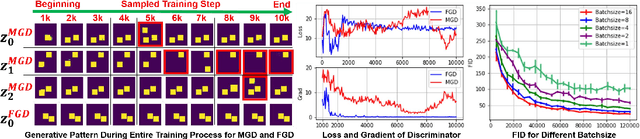

Abstract:Generative models, especially Generative Adversarial Networks (GANs), have received significant attention recently. However, it has been observed that in terms of some attributes, e.g. the number of simple geometric primitives in an image, GANs are not able to learn the target distribution in practice. Motivated by this observation, we discover two specific problems of GANs leading to anomalous generalization behaviour, which we refer to as the sample insufficiency and the pixel-wise combination. For the first problem of sample insufficiency, we show theoretically and empirically that the batchsize of the training samples in practice may be insufficient for the discriminator to learn an accurate discrimination function. It could result in unstable training dynamics for the generator, leading to anomalous generalization. For the second problem of pixel-wise combination, we find that besides recognizing the positive training samples as real, under certain circumstances, the discriminator could be fooled to recognize the pixel-wise combinations (e.g. pixel-wise average) of the positive training samples as real. However, those combinations could be visually different from the real samples in the target distribution. With the fooled discriminator as reference, the generator would obtain biased supervision further, leading to the anomalous generalization behaviour. Additionally, in this paper, we propose methods to mitigate the anomalous generalization of GANs. Extensive experiments on benchmark show our proposed methods improve the FID score up to 30\% on natural image dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge