Multivariate Functional Linear Discriminant Analysis for the Classification of Short Time Series with Missing Data

Functional linear discriminant analysis (FLDA) is a powerful tool that extends LDA-mediated multiclass classification and dimension reduction to univariate time-series functions. However, in the age of large multivariate and incomplete data, statistical dependencies between features must be estimated in a computationally tractable way, while also dealing with missing data. There is a need for a computationally tractable approach that considers the statistical dependencies between features and can handle missing values. We here develop a multivariate version of FLDA (MUDRA) to tackle this issue and describe an efficient expectation/conditional-maximization (ECM) algorithm to infer its parameters. We assess its predictive power on the "Articulary Word Recognition" data set and show its improvement over the state-of-the-art, especially in the case of missing data. MUDRA allows interpretable classification of data sets with large proportions of missing data, which will be particularly useful for medical or psychological data sets.

An Anytime Algorithm for Good Arm Identification

In good arm identification (GAI), the goal is to identify one arm whose average performance exceeds a given threshold, referred to as good arm, if it exists. Few works have studied GAI in the fixed-budget setting, when the sampling budget is fixed beforehand, or the anytime setting, when a recommendation can be asked at any time. We propose APGAI, an anytime and parameter-free sampling rule for GAI in stochastic bandits. APGAI can be straightforwardly used in fixed-confidence and fixed-budget settings. First, we derive upper bounds on its probability of error at any time. They show that adaptive strategies are more efficient in detecting the absence of good arms than uniform sampling. Second, when APGAI is combined with a stopping rule, we prove upper bounds on the expected sampling complexity, holding at any confidence level. Finally, we show good empirical performance of APGAI on synthetic and real-world data. Our work offers an extensive overview of the GAI problem in all settings.

Near-Optimal Collaborative Learning in Bandits

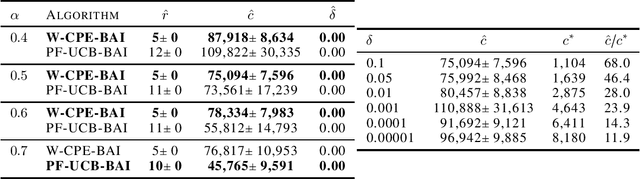
This paper introduces a general multi-agent bandit model in which each agent is facing a finite set of arms and may communicate with other agents through a central controller in order to identify, in pure exploration, or play, in regret minimization, its optimal arm. The twist is that the optimal arm for each agent is the arm with largest expected mixed reward, where the mixed reward of an arm is a weighted sum of the rewards of this arm for all agents. This makes communication between agents often necessary. This general setting allows to recover and extend several recent models for collaborative bandit learning, including the recently proposed federated learning with personalization (Shi et al., 2021). In this paper, we provide new lower bounds on the sample complexity of pure exploration and on the regret. We then propose a near-optimal algorithm for pure exploration. This algorithm is based on phased elimination with two novel ingredients: a data-dependent sampling scheme within each phase, aimed at matching a relaxation of the lower bound.

Dealing With Misspecification In Fixed-Confidence Linear Top-m Identification

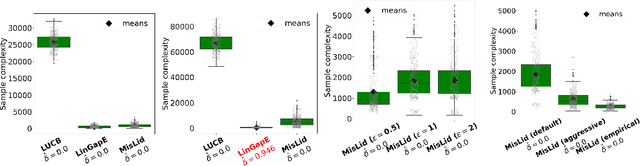
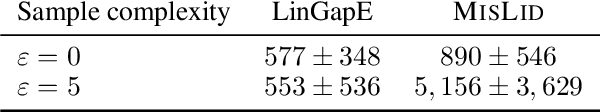
We study the problem of the identification of m arms with largest means under a fixed error rate $\delta$ (fixed-confidence Top-m identification), for misspecified linear bandit models. This problem is motivated by practical applications, especially in medicine and recommendation systems, where linear models are popular due to their simplicity and the existence of efficient algorithms, but in which data inevitably deviates from linearity. In this work, we first derive a tractable lower bound on the sample complexity of any $\delta$-correct algorithm for the general Top-m identification problem. We show that knowing the scale of the deviation from linearity is necessary to exploit the structure of the problem. We then describe the first algorithm for this setting, which is both practical and adapts to the amount of misspecification. We derive an upper bound to its sample complexity which confirms this adaptivity and that matches the lower bound when $\delta$ $\rightarrow$ 0. Finally, we evaluate our algorithm on both synthetic and real-world data, showing competitive performance with respect to existing baselines.

Top-m identification for linear bandits

Motivated by an application to drug repurposing, we propose the first algorithms to tackle the identification of the m $\ge$ 1 arms with largest means in a linear bandit model, in the fixed-confidence setting. These algorithms belong to the generic family of Gap-Index Focused Algorithms (GIFA) that we introduce for Top-m identification in linear bandits. We propose a unified analysis of these algorithms, which shows how the use of features might decrease the sample complexity. We further validate these algorithms empirically on simulated data and on a simple drug repurposing task.