Dealing With Misspecification In Fixed-Confidence Linear Top-m Identification
Paper and Code
Nov 02, 2021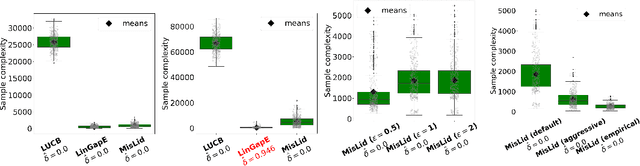


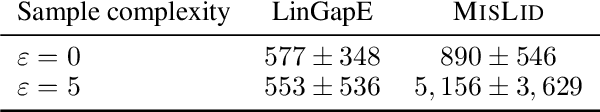
We study the problem of the identification of m arms with largest means under a fixed error rate $\delta$ (fixed-confidence Top-m identification), for misspecified linear bandit models. This problem is motivated by practical applications, especially in medicine and recommendation systems, where linear models are popular due to their simplicity and the existence of efficient algorithms, but in which data inevitably deviates from linearity. In this work, we first derive a tractable lower bound on the sample complexity of any $\delta$-correct algorithm for the general Top-m identification problem. We show that knowing the scale of the deviation from linearity is necessary to exploit the structure of the problem. We then describe the first algorithm for this setting, which is both practical and adapts to the amount of misspecification. We derive an upper bound to its sample complexity which confirms this adaptivity and that matches the lower bound when $\delta$ $\rightarrow$ 0. Finally, we evaluate our algorithm on both synthetic and real-world data, showing competitive performance with respect to existing baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge