Student-t processes as infinite-width limits of posterior Bayesian neural networks

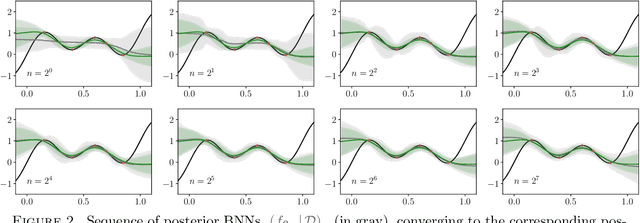
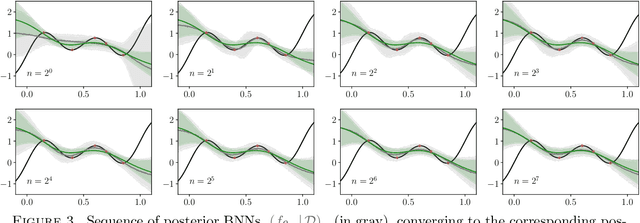
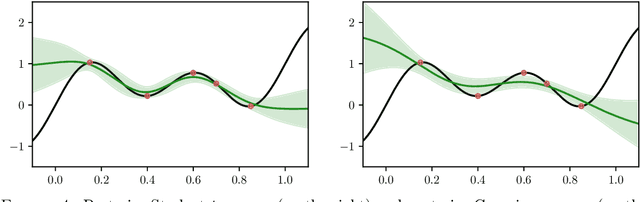
The asymptotic properties of Bayesian Neural Networks (BNNs) have been extensively studied, particularly regarding their approximations by Gaussian processes in the infinite-width limit. We extend these results by showing that posterior BNNs can be approximated by Student-t processes, which offer greater flexibility in modeling uncertainty. Specifically, we show that, if the parameters of a BNN follow a Gaussian prior distribution, and the variance of both the last hidden layer and the Gaussian likelihood function follows an Inverse-Gamma prior distribution, then the resulting posterior BNN converges to a Student-t process in the infinite-width limit. Our proof leverages the Wasserstein metric to establish control over the convergence rate of the Student-t process approximation.

Wide Deep Neural Networks with Gaussian Weights are Very Close to Gaussian Processes

We establish novel rates for the Gaussian approximation of random deep neural networks with Gaussian parameters (weights and biases) and Lipschitz activation functions, in the wide limit. Our bounds apply for the joint output of a network evaluated any finite input set, provided a certain non-degeneracy condition of the infinite-width covariances holds. We demonstrate that the distance between the network output and the corresponding Gaussian approximation scales inversely with the width of the network, exhibiting faster convergence than the naive heuristic suggested by the central limit theorem. We also apply our bounds to obtain theoretical approximations for the exact Bayesian posterior distribution of the network, when the likelihood is a bounded Lipschitz function of the network output evaluated on a (finite) training set. This includes popular cases such as the Gaussian likelihood, i.e. exponential of minus the mean squared error.

Quantitative Gaussian Approximation of Randomly Initialized Deep Neural Networks

Given any deep fully connected neural network, initialized with random Gaussian parameters, we bound from above the quadratic Wasserstein distance between its output distribution and a suitable Gaussian process. Our explicit inequalities indicate how the hidden and output layers sizes affect the Gaussian behaviour of the network and quantitatively recover the distributional convergence results in the wide limit, i.e., if all the hidden layers sizes become large.