Francesco Caporali
Student-t processes as infinite-width limits of posterior Bayesian neural networks
Feb 06, 2025
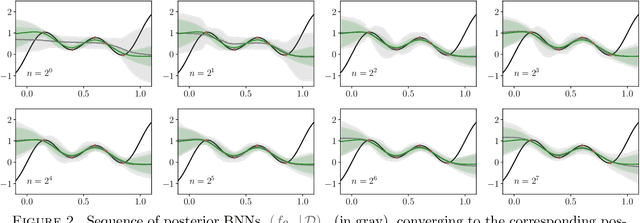
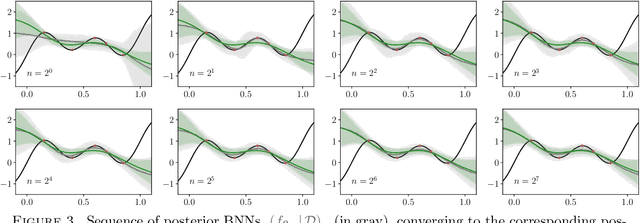
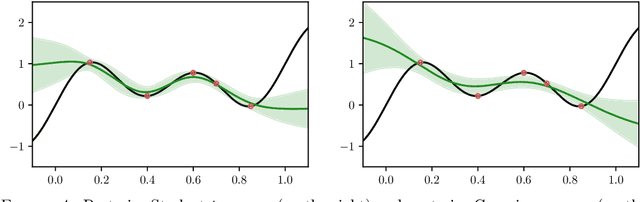
Abstract:The asymptotic properties of Bayesian Neural Networks (BNNs) have been extensively studied, particularly regarding their approximations by Gaussian processes in the infinite-width limit. We extend these results by showing that posterior BNNs can be approximated by Student-t processes, which offer greater flexibility in modeling uncertainty. Specifically, we show that, if the parameters of a BNN follow a Gaussian prior distribution, and the variance of both the last hidden layer and the Gaussian likelihood function follows an Inverse-Gamma prior distribution, then the resulting posterior BNN converges to a Student-t process in the infinite-width limit. Our proof leverages the Wasserstein metric to establish control over the convergence rate of the Student-t process approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge