Fractal and Regular Geometry of Deep Neural Networks

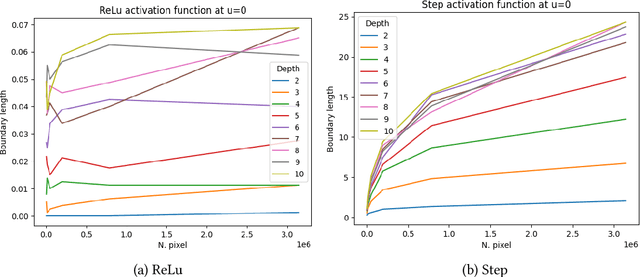
We study the geometric properties of random neural networks by investigating the boundary volumes of their excursion sets for different activation functions, as the depth increases. More specifically, we show that, for activations which are not very regular (e.g., the Heaviside step function), the boundary volumes exhibit fractal behavior, with their Hausdorff dimension monotonically increasing with the depth. On the other hand, for activations which are more regular (e.g., ReLU, logistic and $\tanh$), as the depth increases, the expected boundary volumes can either converge to zero, remain constant or diverge exponentially, depending on a single spectral parameter which can be easily computed. Our theoretical results are confirmed in some numerical experiments based on Monte Carlo simulations.

Spectral complexity of deep neural networks

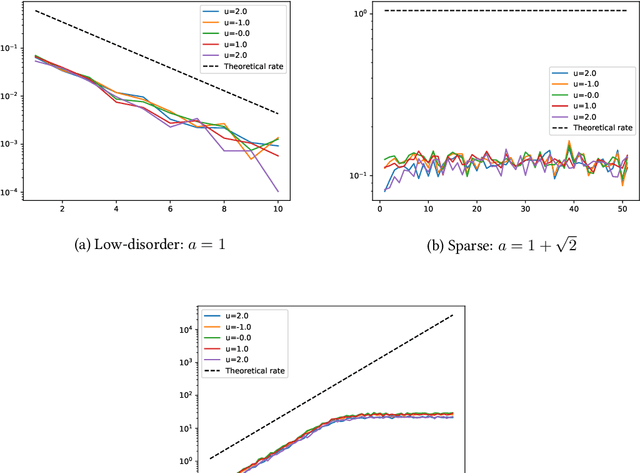
It is well-known that randomly initialized, push-forward, fully-connected neural networks weakly converge to isotropic Gaussian processes, in the limit where the width of all layers goes to infinity. In this paper, we propose to use the angular power spectrum of the limiting field to characterize the complexity of the network architecture. In particular, we define sequences of random variables associated with the angular power spectrum, and provide a full characterization of the network complexity in terms of the asymptotic distribution of these sequences as the depth diverges. On this basis, we classify neural networks as low-disorder, sparse, or high-disorder; we show how this classification highlights a number of distinct features for standard activation functions, and in particular, sparsity properties of ReLU networks. Our theoretical results are also validated by numerical simulations.

Quantitative CLTs in Deep Neural Networks

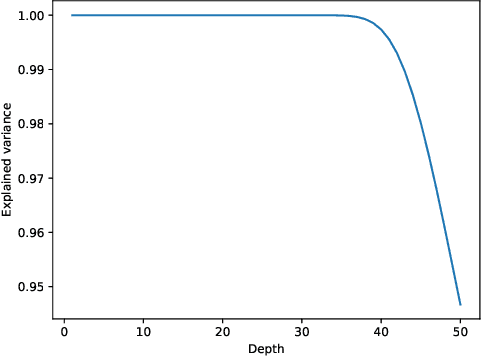
We study the distribution of a fully connected neural network with random Gaussian weights and biases in which the hidden layer widths are proportional to a large constant $n$. Under mild assumptions on the non-linearity, we obtain quantitative bounds on normal approximations valid at large but finite $n$ and any fixed network depth. Our theorems show both for the finite-dimensional distributions and the entire process, that the distance between a random fully connected network (and its derivatives) to the corresponding infinite width Gaussian process scales like $n^{-\gamma}$ for $\gamma>0$, with the exponent depending on the metric used to measure discrepancy. Our bounds are strictly stronger in terms of their dependence on network width than any previously available in the literature; in the one-dimensional case, we also prove that they are optimal, i.e., we establish matching lower bounds.

A Quantitative Functional Central Limit Theorem for Shallow Neural Networks

We prove a Quantitative Functional Central Limit Theorem for one-hidden-layer neural networks with generic activation function. The rates of convergence that we establish depend heavily on the smoothness of the activation function, and they range from logarithmic in non-differentiable cases such as the Relu to $\sqrt{n}$ for very regular activations. Our main tools are functional versions of the Stein-Malliavin approach; in particular, we exploit heavily a quantitative functional central limit theorem which has been recently established by Bourguin and Campese (2020).