Fractal and Regular Geometry of Deep Neural Networks

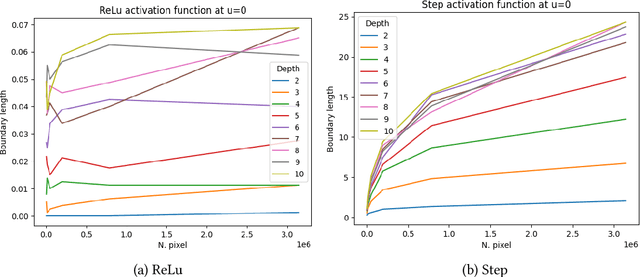
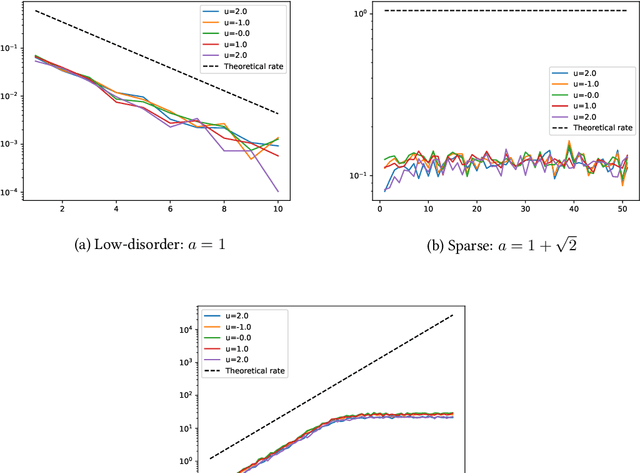
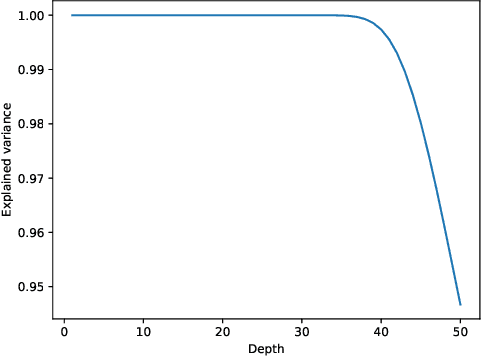
We study the geometric properties of random neural networks by investigating the boundary volumes of their excursion sets for different activation functions, as the depth increases. More specifically, we show that, for activations which are not very regular (e.g., the Heaviside step function), the boundary volumes exhibit fractal behavior, with their Hausdorff dimension monotonically increasing with the depth. On the other hand, for activations which are more regular (e.g., ReLU, logistic and $\tanh$), as the depth increases, the expected boundary volumes can either converge to zero, remain constant or diverge exponentially, depending on a single spectral parameter which can be easily computed. Our theoretical results are confirmed in some numerical experiments based on Monte Carlo simulations.