Critical Points of Random Neural Networks

This work investigates the expected number of critical points of random neural networks with different activation functions as the depth increases in the infinite-width limit. Under suitable regularity conditions, we derive precise asymptotic formulas for the expected number of critical points of fixed index and those exceeding a given threshold. Our analysis reveals three distinct regimes depending on the value of the first derivative of the covariance evaluated at 1: the expected number of critical points may converge, grow polynomially, or grow exponentially with depth. The theoretical predictions are supported by numerical experiments. Moreover, we provide numerical evidence suggesting that, when the regularity condition is not satisfied (e.g. for neural networks with ReLU as activation function), the number of critical points increases as the map resolution increases, indicating a potential divergence in the number of critical points.

Fractal and Regular Geometry of Deep Neural Networks

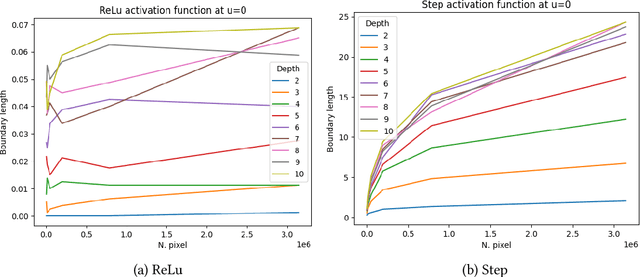
We study the geometric properties of random neural networks by investigating the boundary volumes of their excursion sets for different activation functions, as the depth increases. More specifically, we show that, for activations which are not very regular (e.g., the Heaviside step function), the boundary volumes exhibit fractal behavior, with their Hausdorff dimension monotonically increasing with the depth. On the other hand, for activations which are more regular (e.g., ReLU, logistic and $\tanh$), as the depth increases, the expected boundary volumes can either converge to zero, remain constant or diverge exponentially, depending on a single spectral parameter which can be easily computed. Our theoretical results are confirmed in some numerical experiments based on Monte Carlo simulations.

Spectral complexity of deep neural networks

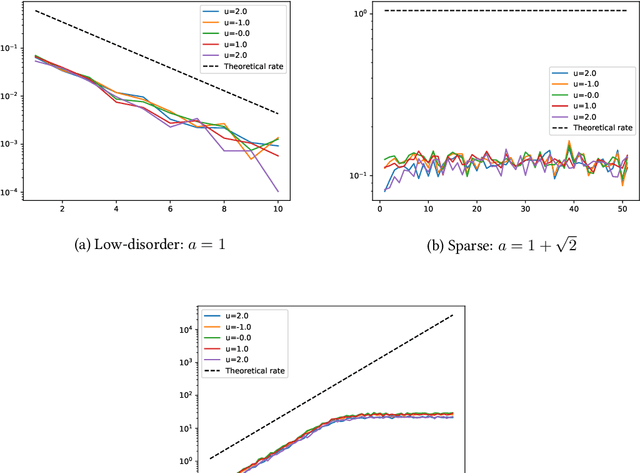
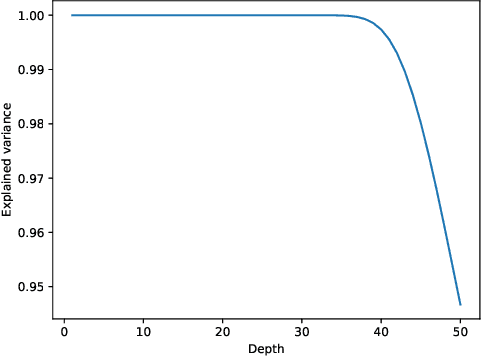
It is well-known that randomly initialized, push-forward, fully-connected neural networks weakly converge to isotropic Gaussian processes, in the limit where the width of all layers goes to infinity. In this paper, we propose to use the angular power spectrum of the limiting field to characterize the complexity of the network architecture. In particular, we define sequences of random variables associated with the angular power spectrum, and provide a full characterization of the network complexity in terms of the asymptotic distribution of these sequences as the depth diverges. On this basis, we classify neural networks as low-disorder, sparse, or high-disorder; we show how this classification highlights a number of distinct features for standard activation functions, and in particular, sparsity properties of ReLU networks. Our theoretical results are also validated by numerical simulations.