An extensive simulation study evaluating the interaction of resampling techniques across multiple causal discovery contexts

Despite the accelerating presence of exploratory causal analysis in modern science and medicine, the available non-experimental methods for validating causal models are not well characterized. One of the most popular methods is to evaluate the stability of model features after resampling the data, similar to resampling methods for estimating confidence intervals in statistics. Many aspects of this approach have received little to no attention, however, such as whether the choice of resampling method should depend on the sample size, algorithms being used, or algorithm tuning parameters. We present theoretical results proving that certain resampling methods closely emulate the assignment of specific values to algorithm tuning parameters. We also report the results of extensive simulation experiments, which verify the theoretical result and provide substantial data to aid researchers in further characterizing resampling in the context of causal discovery analysis. Together, the theoretical work and simulation results provide specific guidance on how resampling methods and tuning parameters should be selected in practice.

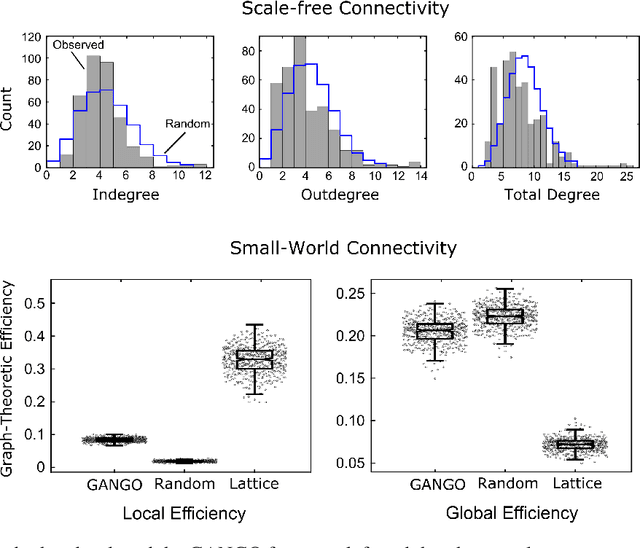
Better Simulations for Validating Causal Discovery with the DAG-Adaptation of the Onion Method

The number of artificial intelligence algorithms for learning causal models from data is growing rapidly. Most ``causal discovery'' or ``causal structure learning'' algorithms are primarily validated through simulation studies. However, no widely accepted simulation standards exist and publications often report conflicting performance statistics -- even when only considering publications that simulate data from linear models. In response, several manuscripts have criticized a popular simulation design for validating algorithms in the linear case. We propose a new simulation design for generating linear models for directed acyclic graphs (DAGs): the DAG-adaptation of the Onion (DaO) method. DaO simulations are fundamentally different from existing simulations because they prioritize the distribution of correlation matrices rather than the distribution of linear effects. Specifically, the DaO method uniformly samples the space of all correlation matrices consistent with (i.e. Markov to) a DAG. We also discuss how to sample DAGs and present methods for generating DAGs with scale-free in-degree or out-degree. We compare the DaO method against two alternative simulation designs and provide implementations of the DaO method in Python and R: https://github.com/bja43/DaO_simulation. We advocate for others to adopt DaO simulations as a fair universal benchmark.

Causal Discovery for fMRI data: Challenges, Solutions, and a Case Study

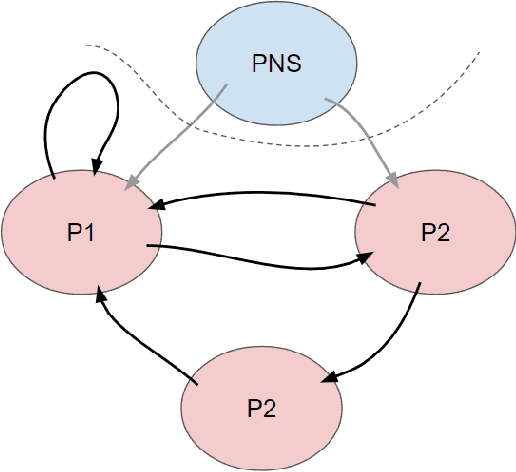
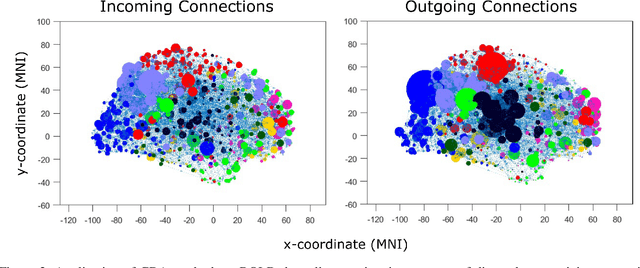
Designing studies that apply causal discovery requires navigating many researcher degrees of freedom. This complexity is exacerbated when the study involves fMRI data. In this paper we (i) describe nine challenges that occur when applying causal discovery to fMRI data, (ii) discuss the space of decisions that need to be made, (iii) review how a recent case study made those decisions, (iv) and identify existing gaps that could potentially be solved by the development of new methods. Overall, causal discovery is a promising approach for analyzing fMRI data, and multiple successful applications have indicated that it is superior to traditional fMRI functional connectivity methods, but current causal discovery methods for fMRI leave room for improvement.

Fast Scalable and Accurate Discovery of DAGs Using the Best Order Score Search and Grow-Shrink Trees

Learning graphical conditional independence structures is an important machine learning problem and a cornerstone of causal discovery. However, the accuracy and execution time of learning algorithms generally struggle to scale to problems with hundreds of highly connected variables -- for instance, recovering brain networks from fMRI data. We introduce the best order score search (BOSS) and grow-shrink trees (GSTs) for learning directed acyclic graphs (DAGs) in this paradigm. BOSS greedily searches over permutations of variables, using GSTs to construct and score DAGs from permutations. GSTs efficiently cache scores to eliminate redundant calculations. BOSS achieves state-of-the-art performance in accuracy and execution time, comparing favorably to a variety of combinatorial and gradient-based learning algorithms under a broad range of conditions. To demonstrate its practicality, we apply BOSS to two sets of resting-state fMRI data: simulated data with pseudo-empirical noise distributions derived from randomized empirical fMRI cortical signals and clinical data from 3T fMRI scans processed into cortical parcels. BOSS is available for use within the TETRAD project which includes Python and R wrappers.

Investigating the effect of binning on causal discovery

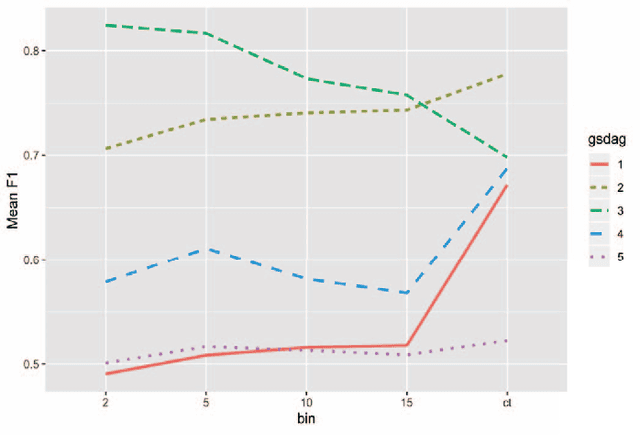
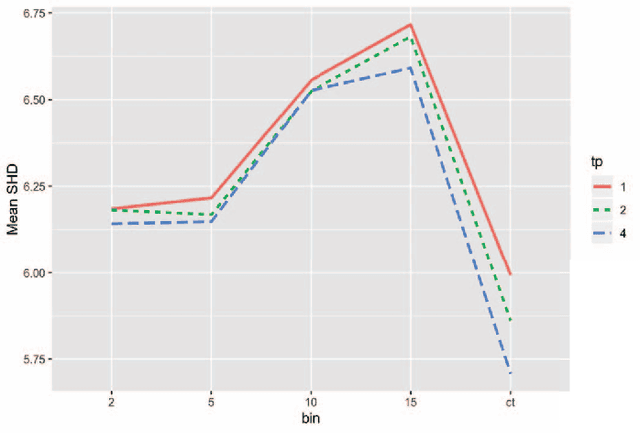
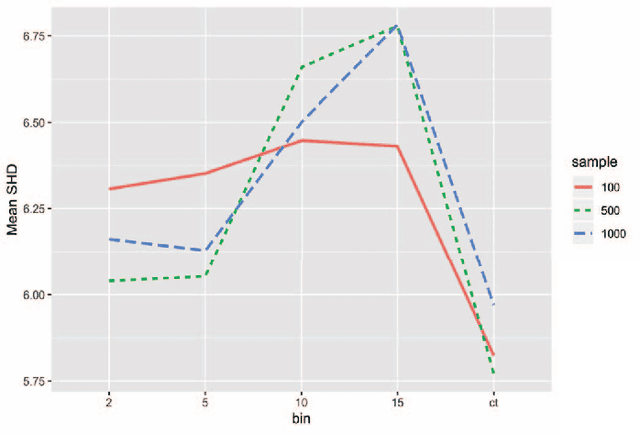
Binning (a.k.a. discretization) of numerically continuous measurements is a wide-spread but controversial practice in data collection, analysis, and presentation. The consequences of binning have been evaluated for many different kinds of data analysis methods, however so far the effect of binning on causal discovery algorithms has not been directly investigated. This paper reports the results of a simulation study that examined the effect of binning on the Greedy Equivalence Search (GES) causal discovery algorithm. Our findings suggest that unbinned continuous data often result in the highest search performance, but some exceptions are identified. We also found that binned data are more sensitive to changes in sample size and tuning parameters, and identified some interactive effects between sample size, binning, and tuning parameter on performance.

A Prospective Observational Study to Investigate Performance of a Chest X-ray Artificial Intelligence Diagnostic Support Tool Across 12 U.S. Hospitals

Importance: An artificial intelligence (AI)-based model to predict COVID-19 likelihood from chest x-ray (CXR) findings can serve as an important adjunct to accelerate immediate clinical decision making and improve clinical decision making. Despite significant efforts, many limitations and biases exist in previously developed AI diagnostic models for COVID-19. Utilizing a large set of local and international CXR images, we developed an AI model with high performance on temporal and external validation. Conclusions and Relevance: AI-based diagnostic tools may serve as an adjunct, but not replacement, for clinical decision support of COVID-19 diagnosis, which largely hinges on exposure history, signs, and symptoms. While AI-based tools have not yet reached full diagnostic potential in COVID-19, they may still offer valuable information to clinicians taken into consideration along with clinical signs and symptoms.

Simulations evaluating resampling methods for causal discovery: ensemble performance and calibration

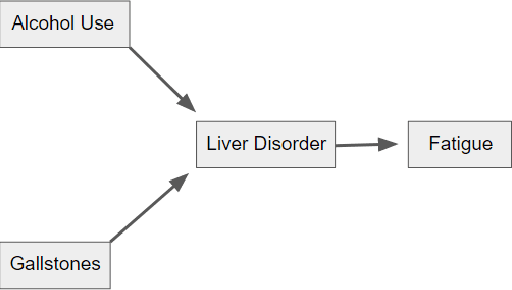
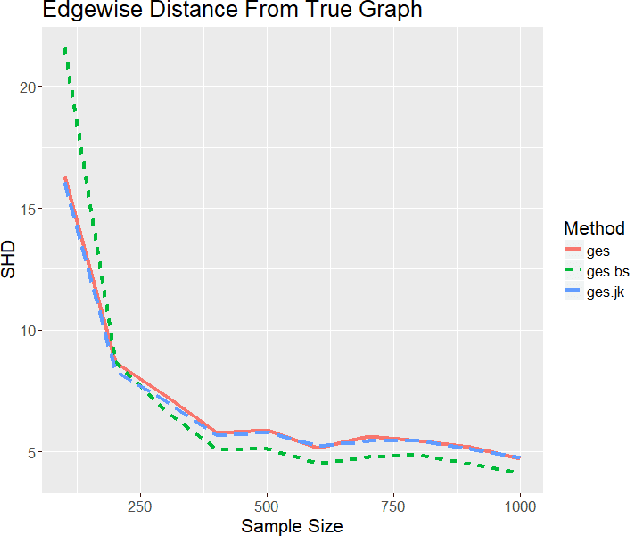
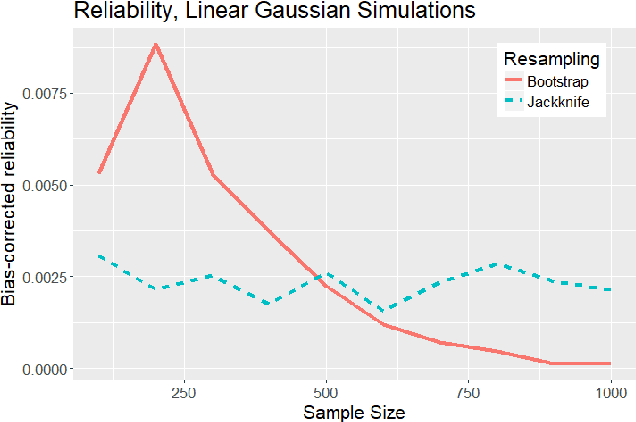
Causal discovery can be a powerful tool for investigating causality when a system can be observed but is inaccessible to experiments in practice. Despite this, it is rarely used in any scientific or medical fields. One of the major hurdles preventing the field of causal discovery from having a larger impact is that it is difficult to determine when the output of a causal discovery method can be trusted in a real-world setting. Trust is especially critical when human health is on the line. In this paper, we report the results of a series of simulation studies investigating the performance of different resampling methods as indicators of confidence in discovered graph features. We found that subsampling and sampling with replacement both performed surprisingly well, suggesting that they can serve as grounds for confidence in graph features. We also found that the calibration of subsampling and sampling with replacement had different convergence properties, suggesting that one's choice of which to use should depend on the sample size.