Jaron Lee
Path Dependent Structural Equation Models
Aug 24, 2020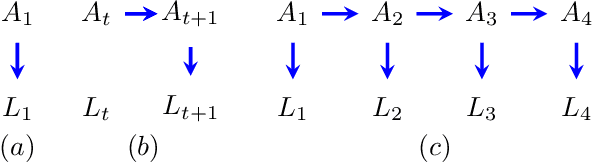
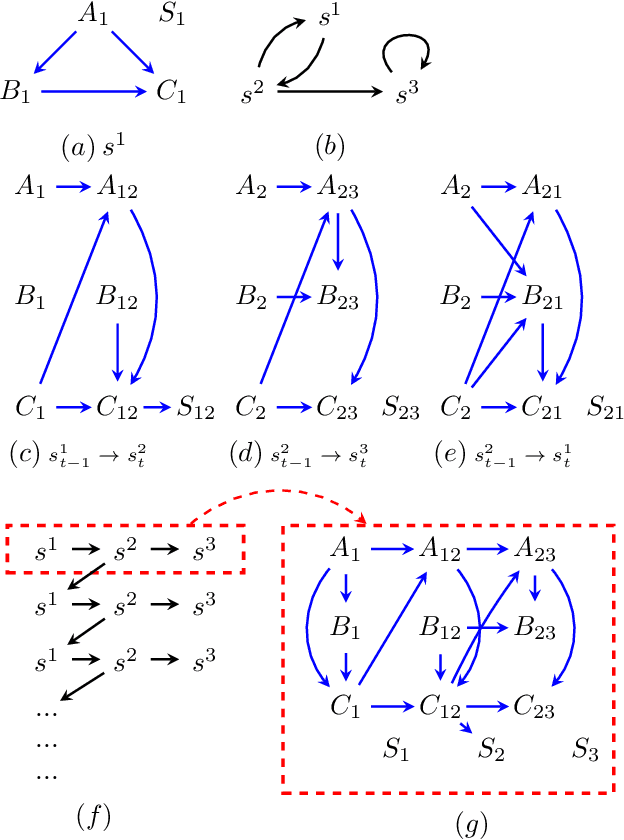
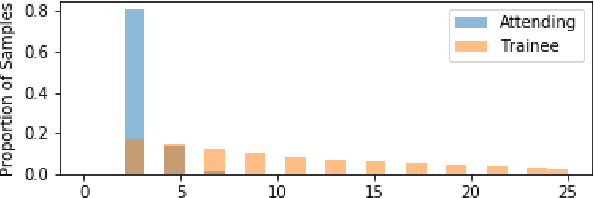
Abstract:Causal analyses of longitudinal data generally assume structure that is invariant over time. Graphical causal models describe these data using a single causal diagram repeated at every time step. In structured systems that transition between qualitatively different states in discrete time steps, such an approach is deficient on two fronts. First, time-varying variables may have state-specific causal relationships that need to be captured. Second, an intervention can result in state transitions downstream of the intervention different from thoseactually observed in the data. In other words, interventions may counterfactually alter the subsequent temporal evolution of the system. We introduce a generalization of causal graphical models, Path Dependent Structural Equation Models (PDSEMs), that can describe such systems. We show how causal inference may be performed in such models and illustrate its use in simulations and data obtained from a septoplasty surgical procedure.
A Semiparametric Approach to Interpretable Machine Learning
Jun 08, 2020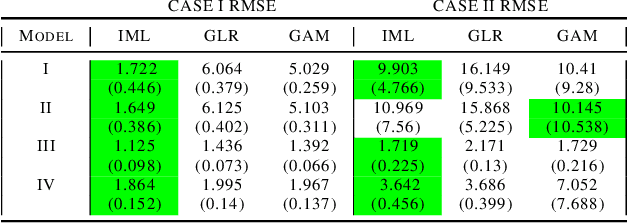


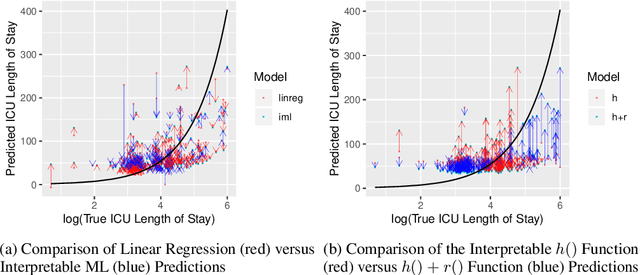
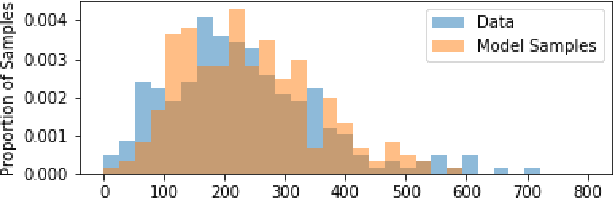
Abstract:Black box models in machine learning have demonstrated excellent predictive performance in complex problems and high-dimensional settings. However, their lack of transparency and interpretability restrict the applicability of such models in critical decision-making processes. In order to combat this shortcoming, we propose a novel approach to trading off interpretability and performance in prediction models using ideas from semiparametric statistics, allowing us to combine the interpretability of parametric regression models with performance of nonparametric methods. We achieve this by utilizing a two-piece model: the first piece is interpretable and parametric, to which a second, uninterpretable residual piece is added. The performance of the overall model is optimized using methods from the sufficient dimension reduction literature. Influence function based estimators are derived and shown to be doubly robust. This allows for use of approaches such as double Machine Learning in estimating our model parameters. We illustrate the utility of our approach via simulation studies and a data application based on predicting the length of stay in the intensive care unit among surgery patients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge