Path Dependent Structural Equation Models
Paper and Code
Aug 24, 2020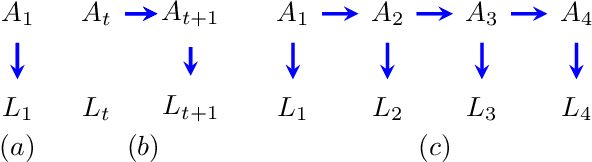
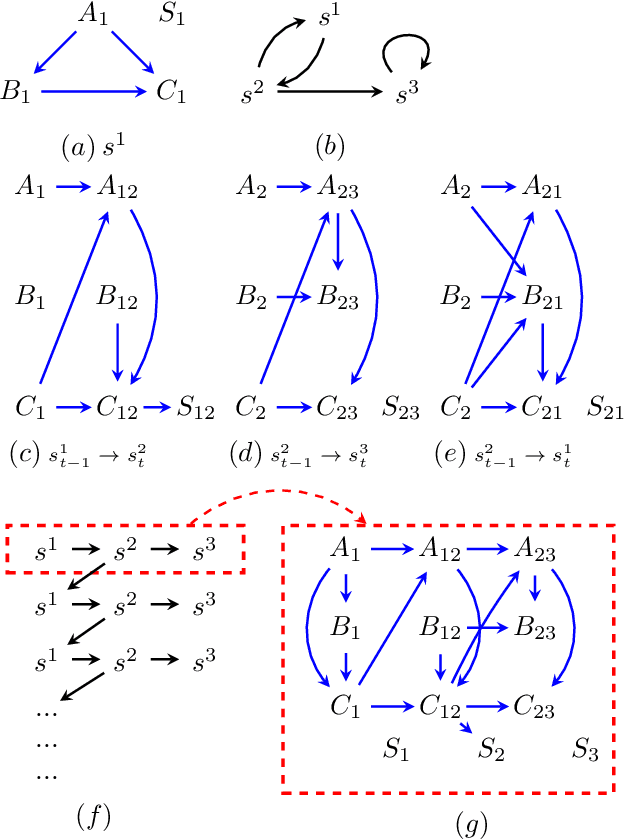
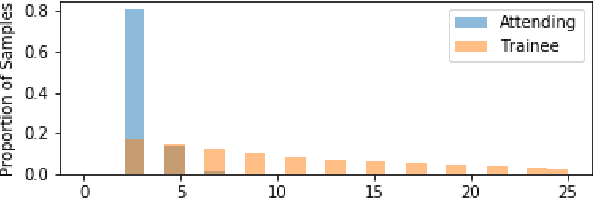
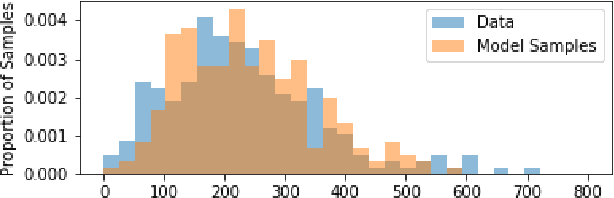
Causal analyses of longitudinal data generally assume structure that is invariant over time. Graphical causal models describe these data using a single causal diagram repeated at every time step. In structured systems that transition between qualitatively different states in discrete time steps, such an approach is deficient on two fronts. First, time-varying variables may have state-specific causal relationships that need to be captured. Second, an intervention can result in state transitions downstream of the intervention different from thoseactually observed in the data. In other words, interventions may counterfactually alter the subsequent temporal evolution of the system. We introduce a generalization of causal graphical models, Path Dependent Structural Equation Models (PDSEMs), that can describe such systems. We show how causal inference may be performed in such models and illustrate its use in simulations and data obtained from a septoplasty surgical procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge