Cross-validating causal discovery via Leave-One-Variable-Out

We propose a new approach to falsify causal discovery algorithms without ground truth, which is based on testing the causal model on a pair of variables that has been dropped when learning the causal model. To this end, we use the "Leave-One-Variable-Out (LOVO)" prediction where $Y$ is inferred from $X$ without any joint observations of $X$ and $Y$, given only training data from $X,Z_1,\dots,Z_k$ and from $Z_1,\dots,Z_k,Y$. We demonstrate that causal models on the two subsets, in the form of Acyclic Directed Mixed Graphs (ADMGs), often entail conclusions on the dependencies between $X$ and $Y$, enabling this type of prediction. The prediction error can then be estimated since the joint distribution $P(X, Y)$ is assumed to be available, and $X$ and $Y$ have only been omitted for the purpose of falsification. After presenting this graphical method, which is applicable to general causal discovery algorithms, we illustrate how to construct a LOVO predictor tailored towards algorithms relying on specific a priori assumptions, such as linear additive noise models. Simulations indicate that the LOVO prediction error is indeed correlated with the accuracy of the causal outputs, affirming the method's effectiveness.

Anytime-Valid Inference for Double/Debiased Machine Learning of Causal Parameters

Double (debiased) machine learning (DML) has seen widespread use in recent years for learning causal/structural parameters, in part due to its flexibility and adaptability to high-dimensional nuisance functions as well as its ability to avoid bias from regularization or overfitting. However, the classic double-debiased framework is only valid asymptotically for a predetermined sample size, thus lacking the flexibility of collecting more data if sharper inference is needed, or stopping data collection early if useful inferences can be made earlier than expected. This can be of particular concern in large scale experimental studies with huge financial costs or human lives at stake, as well as in observational studies where the length of confidence of intervals do not shrink to zero even with increasing sample size due to partial identifiability of a structural parameter. In this paper, we present time-uniform counterparts to the asymptotic DML results, enabling valid inference and confidence intervals for structural parameters to be constructed at any arbitrary (possibly data-dependent) stopping time. We provide conditions which are only slightly stronger than the standard DML conditions, but offer the stronger guarantee for anytime-valid inference. This facilitates the transformation of any existing DML method to provide anytime-valid guarantees with minimal modifications, making it highly adaptable and easy to use. We illustrate our procedure using two instances: a) local average treatment effect in online experiments with non-compliance, and b) partial identification of average treatment effect in observational studies with potential unmeasured confounding.

Root Cause Analysis of Outliers with Missing Structural Knowledge

Recent work conceptualized root cause analysis (RCA) of anomalies via quantitative contribution analysis using causal counterfactuals in structural causal models (SCMs). The framework comes with three practical challenges: (1) it requires the causal directed acyclic graph (DAG), together with an SCM, (2) it is statistically ill-posed since it probes regression models in regions of low probability density, (3) it relies on Shapley values which are computationally expensive to find. In this paper, we propose simplified, efficient methods of root cause analysis when the task is to identify a unique root cause instead of quantitative contribution analysis. Our proposed methods run in linear order of SCM nodes and they require only the causal DAG without counterfactuals. Furthermore, for those use cases where the causal DAG is unknown, we justify the heuristic of identifying root causes as the variables with the highest anomaly score.

The PetShop Dataset -- Finding Causes of Performance Issues across Microservices

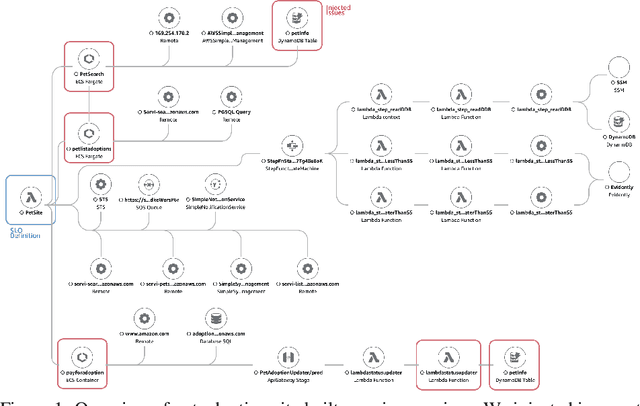
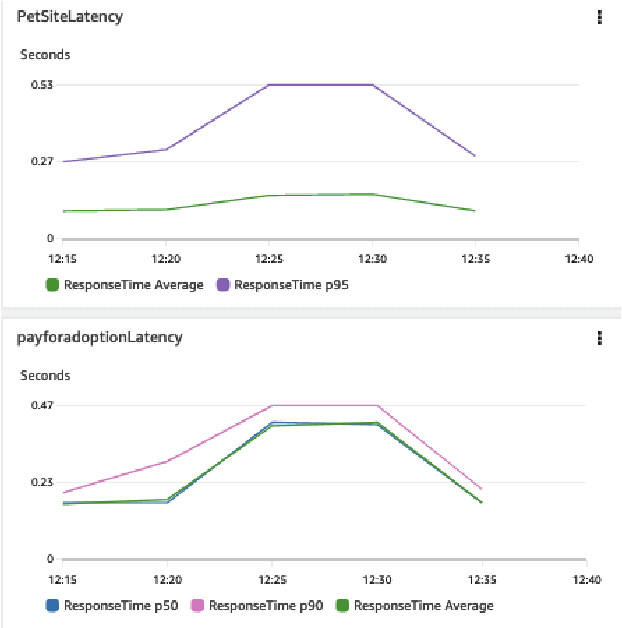
Identifying root causes for unexpected or undesirable behavior in complex systems is a prevalent challenge. This issue becomes especially crucial in modern cloud applications that employ numerous microservices. Although the machine learning and systems research communities have proposed various techniques to tackle this problem, there is currently a lack of standardized datasets for quantitative benchmarking. Consequently, research groups are compelled to create their own datasets for experimentation. This paper introduces a dataset specifically designed for evaluating root cause analyses in microservice-based applications. The dataset encompasses latency, requests, and availability metrics emitted in 5-minute intervals from a distributed application. In addition to normal operation metrics, the dataset includes 68 injected performance issues, which increase latency and reduce availability throughout the system. We showcase how this dataset can be used to evaluate the accuracy of a variety of methods spanning different causal and non-causal characterisations of the root cause analysis problem. We hope the new dataset, available at https://github.com/amazon-science/petshop-root-cause-analysis/ enables further development of techniques in this important area.

Beyond Single-Feature Importance with ICECREAM

Which set of features was responsible for a certain output of a machine learning model? Which components caused the failure of a cloud computing application? These are just two examples of questions we are addressing in this work by Identifying Coalition-based Explanations for Common and Rare Events in Any Model (ICECREAM). Specifically, we propose an information-theoretic quantitative measure for the influence of a coalition of variables on the distribution of a target variable. This allows us to identify which set of factors is essential to obtain a certain outcome, as opposed to well-established explainability and causal contribution analysis methods which can assign contributions only to individual factors and rank them by their importance. In experiments with synthetic and real-world data, we show that ICECREAM outperforms state-of-the-art methods for explainability and root cause analysis, and achieves impressive accuracy in both tasks.

Toward Falsifying Causal Graphs Using a Permutation-Based Test

Understanding the causal relationships among the variables of a system is paramount to explain and control its behaviour. Inferring the causal graph from observational data without interventions, however, requires a lot of strong assumptions that are not always realistic. Even for domain experts it can be challenging to express the causal graph. Therefore, metrics that quantitatively assess the goodness of a causal graph provide helpful checks before using it in downstream tasks. Existing metrics provide an absolute number of inconsistencies between the graph and the observed data, and without a baseline, practitioners are left to answer the hard question of how many such inconsistencies are acceptable or expected. Here, we propose a novel consistency metric by constructing a surrogate baseline through node permutations. By comparing the number of inconsistencies with those on the surrogate baseline, we derive an interpretable metric that captures whether the DAG fits significantly better than random. Evaluating on both simulated and real data sets from various domains, including biology and cloud monitoring, we demonstrate that the true DAG is not falsified by our metric, whereas the wrong graphs given by a hypothetical user are likely to be falsified.

Interventional and Counterfactual Inference with Diffusion Models

We consider the problem of answering observational, interventional, and counterfactual queries in a causally sufficient setting where only observational data and the causal graph are available. Utilizing the recent developments in diffusion models, we introduce diffusion-based causal models (DCM) to learn causal mechanisms, that generate unique latent encodings to allow for direct sampling under interventions as well as abduction for counterfactuals. We utilize DCM to model structural equations, seeing that diffusion models serve as a natural candidate here since they encode each node to a latent representation, a proxy for the exogenous noise, and offer flexible and accurate modeling to provide reliable causal statements and estimates. Our empirical evaluations demonstrate significant improvements over existing state-of-the-art methods for answering causal queries. Our theoretical results provide a methodology for analyzing the counterfactual error for general encoder/decoder models which could be of independent interest.

Thompson Sampling with Diffusion Generative Prior

In this work, we initiate the idea of using denoising diffusion models to learn priors for online decision making problems. Our special focus is on the meta-learning for bandit framework, with the goal of learning a strategy that performs well across bandit tasks of a same class. To this end, we train a diffusion model that learns the underlying task distribution and combine Thompson sampling with the learned prior to deal with new tasks at test time. Our posterior sampling algorithm is designed to carefully balance between the learned prior and the noisy observations that come from the learner's interaction with the environment. To capture realistic bandit scenarios, we also propose a novel diffusion model training procedure that trains even from incomplete and/or noisy data, which could be of independent interest. Finally, our extensive experimental evaluations clearly demonstrate the potential of the proposed approach.

Manifold Restricted Interventional Shapley Values

Shapley values are model-agnostic methods for explaining model predictions. Many commonly used methods of computing Shapley values, known as \emph{off-manifold methods}, rely on model evaluations on out-of-distribution input samples. Consequently, explanations obtained are sensitive to model behaviour outside the data distribution, which may be irrelevant for all practical purposes. While \emph{on-manifold methods} have been proposed which do not suffer from this problem, we show that such methods are overly dependent on the input data distribution, and therefore result in unintuitive and misleading explanations. To circumvent these problems, we propose \emph{ManifoldShap}, which respects the model's domain of validity by restricting model evaluations to the data manifold. We show, theoretically and empirically, that ManifoldShap is robust to off-manifold perturbations of the model and leads to more accurate and intuitive explanations than existing state-of-the-art Shapley methods.

Sequential Kernelized Independence Testing

Independence testing is a fundamental and classical statistical problem that has been extensively studied in the batch setting when one fixes the sample size before collecting data. However, practitioners often prefer procedures that adapt to the complexity of a problem at hand instead of setting sample size in advance. Ideally, such procedures should (a) allow stopping earlier on easy tasks (and later on harder tasks), hence making better use of available resources, and (b) continuously monitor the data and efficiently incorporate statistical evidence after collecting new data, while controlling the false alarm rate. It is well known that classical batch tests are not tailored for streaming data settings, since valid inference after data peeking requires correcting for multiple testing, but such corrections generally result in low power. In this paper, we design sequential kernelized independence tests (SKITs) that overcome such shortcomings based on the principle of testing by betting. We exemplify our broad framework using bets inspired by kernelized dependence measures such as the Hilbert-Schmidt independence criterion (HSIC) and the constrained-covariance criterion (COCO). Importantly, we also generalize the framework to non-i.i.d. time-varying settings, for which there exist no batch tests. We demonstrate the power of our approaches on both simulated and real data.