Manifold Restricted Interventional Shapley Values

Shapley values are model-agnostic methods for explaining model predictions. Many commonly used methods of computing Shapley values, known as \emph{off-manifold methods}, rely on model evaluations on out-of-distribution input samples. Consequently, explanations obtained are sensitive to model behaviour outside the data distribution, which may be irrelevant for all practical purposes. While \emph{on-manifold methods} have been proposed which do not suffer from this problem, we show that such methods are overly dependent on the input data distribution, and therefore result in unintuitive and misleading explanations. To circumvent these problems, we propose \emph{ManifoldShap}, which respects the model's domain of validity by restricting model evaluations to the data manifold. We show, theoretically and empirically, that ManifoldShap is robust to off-manifold perturbations of the model and leads to more accurate and intuitive explanations than existing state-of-the-art Shapley methods.

Unsupervised Model Selection for Time-series Anomaly Detection

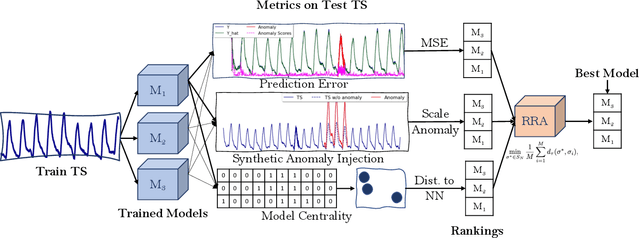
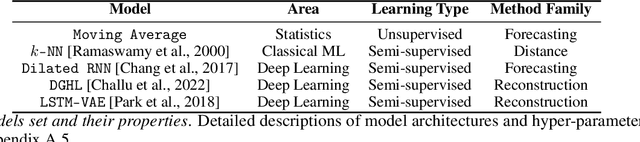
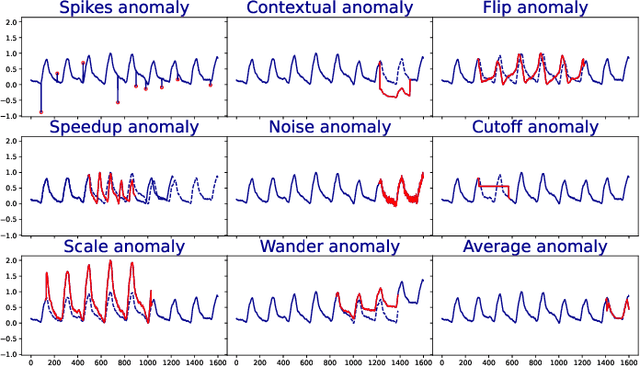
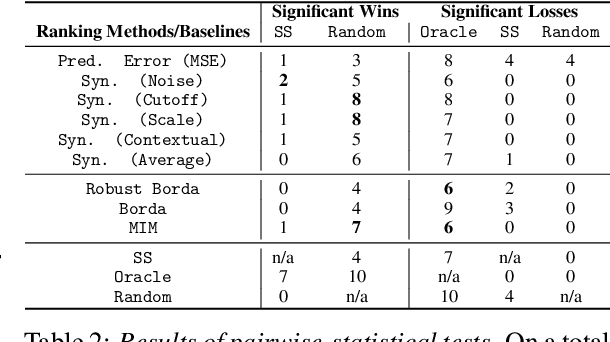
Anomaly detection in time-series has a wide range of practical applications. While numerous anomaly detection methods have been proposed in the literature, a recent survey concluded that no single method is the most accurate across various datasets. To make matters worse, anomaly labels are scarce and rarely available in practice. The practical problem of selecting the most accurate model for a given dataset without labels has received little attention in the literature. This paper answers this question i.e. Given an unlabeled dataset and a set of candidate anomaly detectors, how can we select the most accurate model? To this end, we identify three classes of surrogate (unsupervised) metrics, namely, prediction error, model centrality, and performance on injected synthetic anomalies, and show that some metrics are highly correlated with standard supervised anomaly detection performance metrics such as the $F_1$ score, but to varying degrees. We formulate metric combination with multiple imperfect surrogate metrics as a robust rank aggregation problem. We then provide theoretical justification behind the proposed approach. Large-scale experiments on multiple real-world datasets demonstrate that our proposed unsupervised approach is as effective as selecting the most accurate model based on partially labeled data.

Testing Granger Non-Causality in Panels with Cross-Sectional Dependencies

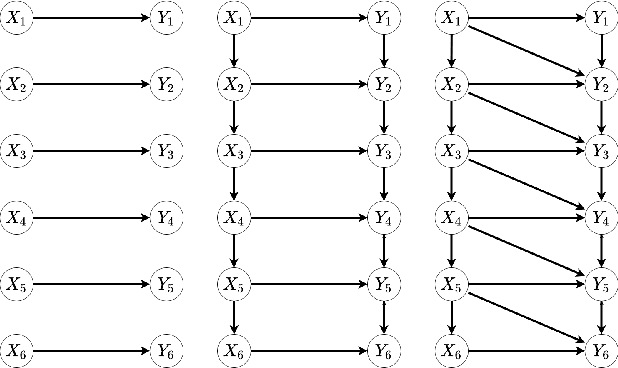
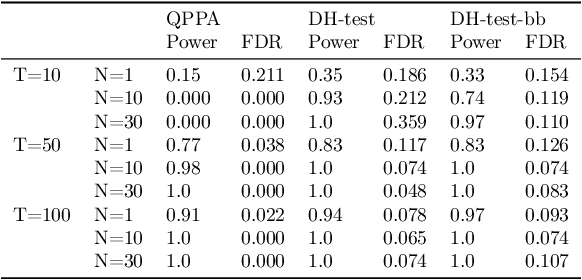
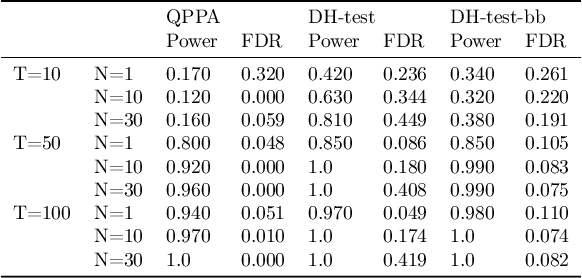
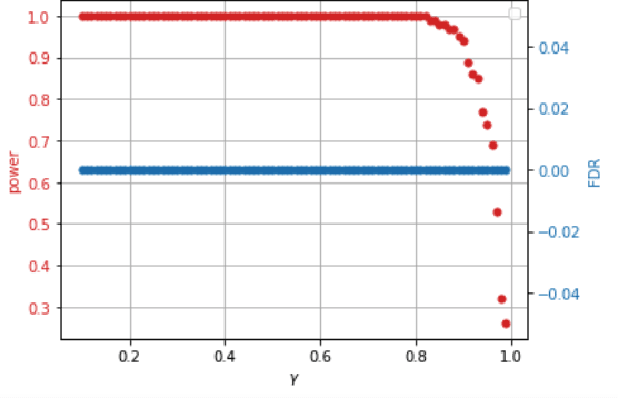
This paper proposes a new approach for testing Granger non-causality on panel data. Instead of aggregating panel member statistics, we aggregate their corresponding p-values and show that the resulting p-value approximately bounds the type I error by the chosen significance level even if the panel members are dependent. We compare our approach against the most widely used Granger causality algorithm on panel data and show that our approach yields lower FDR at the same power for large sample sizes and panels with cross-sectional dependencies. Finally, we examine COVID-19 data about confirmed cases and deaths measured in countries/regions worldwide and show that our approach is able to discover the true causal relation between confirmed cases and deaths while state-of-the-art approaches fail.

Correcting Confounding via Random Selection of Background Variables

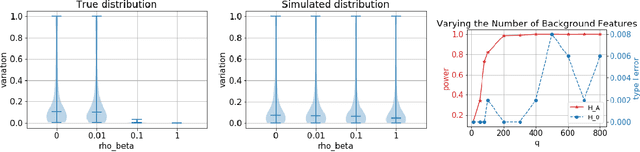
We propose a method to distinguish causal influence from hidden confounding in the following scenario: given a target variable Y, potential causal drivers X, and a large number of background features, we propose a novel criterion for identifying causal relationship based on the stability of regression coefficients of X on Y with respect to selecting different background features. To this end, we propose a statistic V measuring the coefficient's variability. We prove, subject to a symmetry assumption for the background influence, that V converges to zero if and only if X contains no causal drivers. In experiments with simulated data, the method outperforms state of the art algorithms. Further, we report encouraging results for real-world data. Our approach aligns with the general belief that causal insights admit better generalization of statistical associations across environments, and justifies similar existing heuristic approaches from the literature.

Causal Forecasting:Generalization Bounds for Autoregressive Models

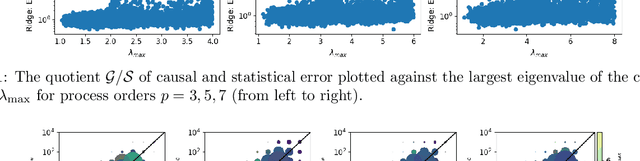
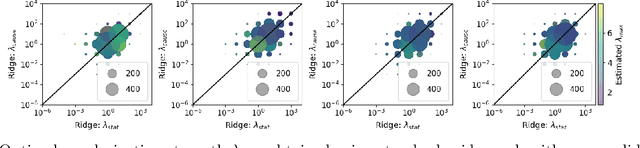
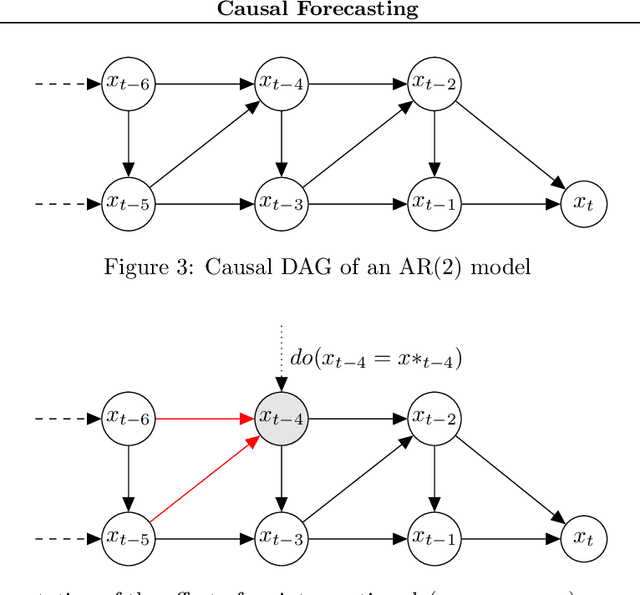
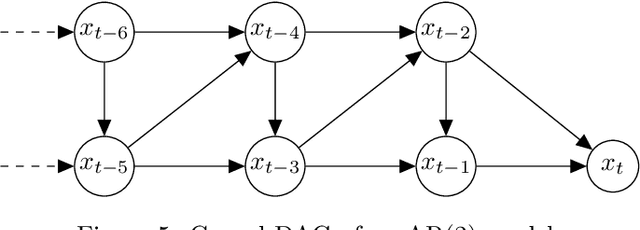
Despite the increasing relevance of forecasting methods, the causal implications of these algorithms remain largely unexplored. This is concerning considering that, even under simplifying assumptions such as causal sufficiency, the statistical risk of a model can differ significantly from its \textit{causal risk}. Here, we study the problem of *causal generalization* -- generalizing from the observational to interventional distributions -- in forecasting. Our goal is to find answers to the question: How does the efficacy of an autoregressive (VAR) model in predicting statistical associations compare with its ability to predict under interventions? To this end, we introduce the framework of *causal learning theory* for forecasting. Using this framework, we obtain a characterization of the difference between statistical and causal risks, which helps identify sources of divergence between them. Under causal sufficiency, the problem of causal generalization amounts to learning under covariate shifts albeit with additional structure (restriction to interventional distributions). This structure allows us to obtain uniform convergence bounds on causal generalizability for the class of VAR models. To the best of our knowledge, this is the first work that provides theoretical guarantees for causal generalization in the time-series setting.

Quantifying causal contribution via structure preserving interventions

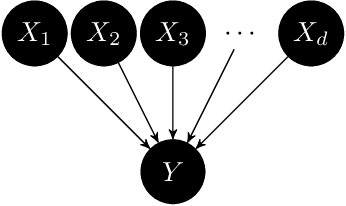
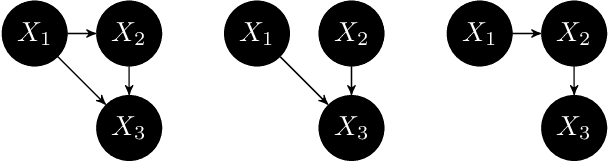
We introduce 'Causal Information Contribution (CIC)' and 'Causal Variance Contribution (CVC)' to quantify the influence of each variable in a causal directed acyclic graph on some target variable. CIC is based on the underlying Functional Causal Model (FCM), in which we define 'structure preserving interventions' as those that act on the unobserved noise variables only. This way, we obtain a measure of influence that quantifies the contribution of each node in its 'normal operation mode'. The total uncertainty of a target variable (measured in terms of variance or Shannon entropy) can then be attributed to the information from each noise term via Shapley values. CIC and CVC are inspired by Analysis of Variance (ANOVA), but also applies to non-linear influence with causally dependent causes.

Causal structure based root cause analysis of outliers

We describe a formal approach to identify 'root causes' of outliers observed in $n$ variables $X_1,\dots,X_n$ in a scenario where the causal relation between the variables is a known directed acyclic graph (DAG). To this end, we first introduce a systematic way to define outlier scores. Further, we introduce the concept of 'conditional outlier score' which measures whether a value of some variable is unexpected *given the value of its parents* in the DAG, if one were to assume that the causal structure and the corresponding conditional distributions are also valid for the anomaly. Finally, we quantify to what extent the high outlier score of some target variable can be attributed to outliers of its ancestors. This quantification is defined via Shapley values from cooperative game theory.

Feature relevance quantification in explainable AI: A causal problem

We discuss promising recent contributions on quantifying feature relevance using Shapley values, where we observed some confusion on which probability distribution is the right one for dropped features. We argue that the confusion is based on not carefully distinguishing between observational and interventional conditional probabilities and try a clarification based on Pearl's seminal work on causality. We conclude that unconditional rather than conditional expectations provide the right notion of dropping features in contradiction to the theoretical justification of the software package SHAP. Parts of SHAP are unaffected because unconditional expectations (which we argue to be conceptually right) are used as approximation for the conditional ones, which encouraged others to `improve' SHAP in a way that we believe to be flawed.