Quantifying causal contribution via structure preserving interventions

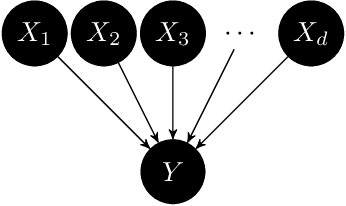
We introduce 'Causal Information Contribution (CIC)' and 'Causal Variance Contribution (CVC)' to quantify the influence of each variable in a causal directed acyclic graph on some target variable. CIC is based on the underlying Functional Causal Model (FCM), in which we define 'structure preserving interventions' as those that act on the unobserved noise variables only. This way, we obtain a measure of influence that quantifies the contribution of each node in its 'normal operation mode'. The total uncertainty of a target variable (measured in terms of variance or Shannon entropy) can then be attributed to the information from each noise term via Shapley values. CIC and CVC are inspired by Analysis of Variance (ANOVA), but also applies to non-linear influence with causally dependent causes.