Correcting Confounding via Random Selection of Background Variables

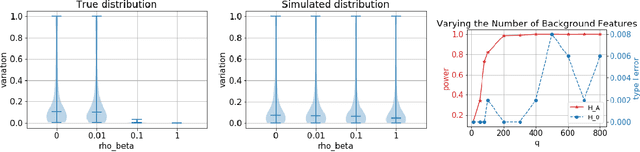
We propose a method to distinguish causal influence from hidden confounding in the following scenario: given a target variable Y, potential causal drivers X, and a large number of background features, we propose a novel criterion for identifying causal relationship based on the stability of regression coefficients of X on Y with respect to selecting different background features. To this end, we propose a statistic V measuring the coefficient's variability. We prove, subject to a symmetry assumption for the background influence, that V converges to zero if and only if X contains no causal drivers. In experiments with simulated data, the method outperforms state of the art algorithms. Further, we report encouraging results for real-world data. Our approach aligns with the general belief that causal insights admit better generalization of statistical associations across environments, and justifies similar existing heuristic approaches from the literature.

Provably Training Neural Network Classifiers under Fairness Constraints

Training a classifier under fairness constraints has gotten increasing attention in the machine learning community thanks to moral, legal, and business reasons. However, several recent works addressing algorithmic fairness have only focused on simple models such as logistic regression or support vector machines due to non-convex and non-differentiable fairness criteria across protected groups, such as race or gender. Neural networks, the most widely used models for classification nowadays, are precluded and lack theoretical guarantees. This paper aims to fill this missing but crucial part of the literature of algorithmic fairness for neural networks. In particular, we show that overparametrized neural networks could meet the fairness constraints. The key ingredient of building a fair neural network classifier is establishing no-regret analysis for neural networks in the overparameterization regime, which may be of independent interest in the online learning of neural networks and related applications.

Provably Efficient Neural Estimation of Structural Equation Model: An Adversarial Approach

Structural equation models (SEMs) are widely used in sciences, ranging from economics to psychology, to uncover causal relationships underlying a complex system under consideration and estimate structural parameters of interest. We study estimation in a class of generalized SEMs where the object of interest is defined as the solution to a linear operator equation. We formulate the linear operator equation as a min-max game, where both players are parameterized by neural networks (NNs), and learn the parameters of these neural networks using the stochastic gradient descent. We consider both 2-layer and multi-layer NNs with ReLU activation functions and prove global convergence in an overparametrized regime, where the number of neurons is diverging. The results are established using techniques from online learning and local linearization of NNs, and improve in several aspects the current state-of-the-art. For the first time we provide a tractable estimation procedure for SEMs based on NNs with provable convergence and without the need for sample splitting.

Tensor Canonical Correlation Analysis

In many applications, such as classification of images or videos, it is of interest to develop a framework for tensor data instead of ad-hoc way of transforming data to vectors due to the computational and under-sampling issues. In this paper, we study canonical correlation analysis by extending the framework of two dimensional analysis (Lee and Choi, 2007) to tensor-valued data. Instead of adopting the iterative algorithm provided in Lee and Choi (2007), we propose an efficient algorithm, called the higher-order power method, which is commonly used in tensor decomposition and more efficient for large-scale setting. Moreover, we carefully examine theoretical properties of our algorithm and establish a local convergence property via the theory of Lojasiewicz's inequalities. Our results fill a missing, but crucial, part in the literature on tensor data. For practical applications, we further develop (a) an inexact updating scheme which allows us to use the state-of-the-art stochastic gradient descent algorithm, (b) an effective initialization scheme which alleviates the problem of local optimum in non-convex optimization, and (c) an extension for extracting several canonical components. Empirical analyses on challenging data including gene expression, air pollution indexes in Taiwan, and electricity demand in Australia, show the effectiveness and efficiency of the proposed methodology.