Anytime-Valid Inference for Double/Debiased Machine Learning of Causal Parameters

Double (debiased) machine learning (DML) has seen widespread use in recent years for learning causal/structural parameters, in part due to its flexibility and adaptability to high-dimensional nuisance functions as well as its ability to avoid bias from regularization or overfitting. However, the classic double-debiased framework is only valid asymptotically for a predetermined sample size, thus lacking the flexibility of collecting more data if sharper inference is needed, or stopping data collection early if useful inferences can be made earlier than expected. This can be of particular concern in large scale experimental studies with huge financial costs or human lives at stake, as well as in observational studies where the length of confidence of intervals do not shrink to zero even with increasing sample size due to partial identifiability of a structural parameter. In this paper, we present time-uniform counterparts to the asymptotic DML results, enabling valid inference and confidence intervals for structural parameters to be constructed at any arbitrary (possibly data-dependent) stopping time. We provide conditions which are only slightly stronger than the standard DML conditions, but offer the stronger guarantee for anytime-valid inference. This facilitates the transformation of any existing DML method to provide anytime-valid guarantees with minimal modifications, making it highly adaptable and easy to use. We illustrate our procedure using two instances: a) local average treatment effect in online experiments with non-compliance, and b) partial identification of average treatment effect in observational studies with potential unmeasured confounding.

The PetShop Dataset -- Finding Causes of Performance Issues across Microservices

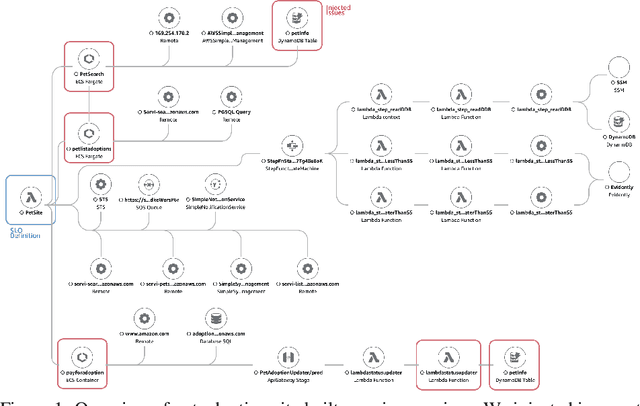
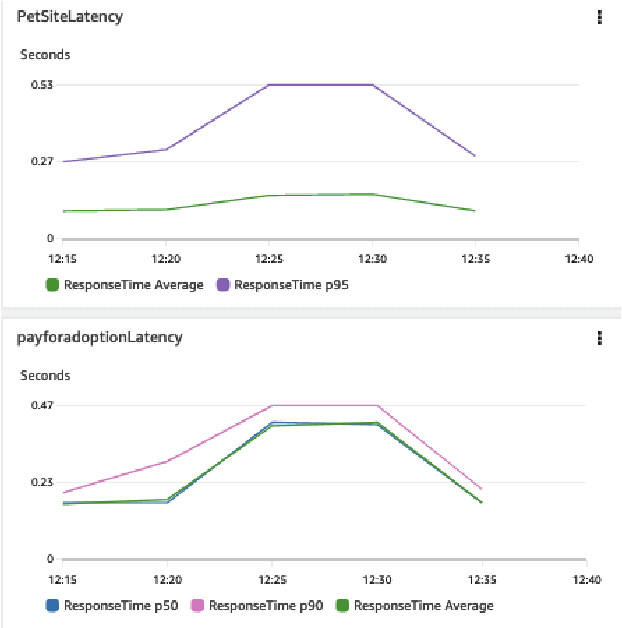
Identifying root causes for unexpected or undesirable behavior in complex systems is a prevalent challenge. This issue becomes especially crucial in modern cloud applications that employ numerous microservices. Although the machine learning and systems research communities have proposed various techniques to tackle this problem, there is currently a lack of standardized datasets for quantitative benchmarking. Consequently, research groups are compelled to create their own datasets for experimentation. This paper introduces a dataset specifically designed for evaluating root cause analyses in microservice-based applications. The dataset encompasses latency, requests, and availability metrics emitted in 5-minute intervals from a distributed application. In addition to normal operation metrics, the dataset includes 68 injected performance issues, which increase latency and reduce availability throughout the system. We showcase how this dataset can be used to evaluate the accuracy of a variety of methods spanning different causal and non-causal characterisations of the root cause analysis problem. We hope the new dataset, available at https://github.com/amazon-science/petshop-root-cause-analysis/ enables further development of techniques in this important area.

Contextual Online False Discovery Rate Control

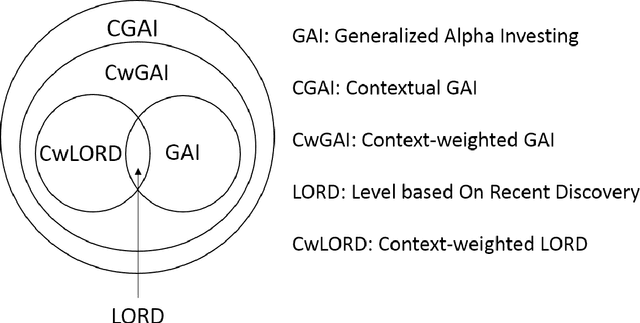
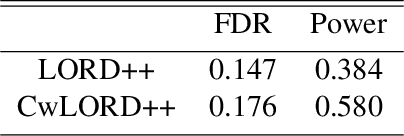
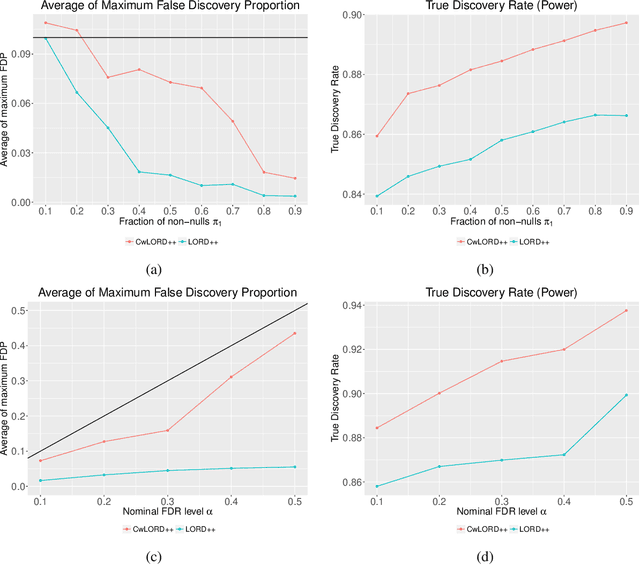
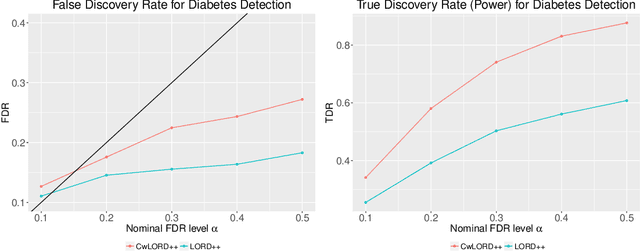
Multiple hypothesis testing, a situation when we wish to consider many hypotheses, is a core problem in statistical inference that arises in almost every scientific field. In this setting, controlling the false discovery rate (FDR), which is the expected proportion of type I error, is an important challenge for making meaningful inferences. In this paper, we consider the problem of controlling FDR in an online manner. Concretely, we consider an ordered, possibly infinite, sequence of hypotheses, arriving one at each timestep, and for each hypothesis we observe a p-value along with a set of features specific to that hypothesis. The decision whether or not to reject the current hypothesis must be made immediately at each timestep, before the next hypothesis is observed. The model of multi-dimensional feature set provides a very general way of leveraging the auxiliary information in the data which helps in maximizing the number of discoveries. We propose a new class of powerful online testing procedures, where the rejections thresholds (significance levels) are learnt sequentially by incorporating contextual information and previous results. We prove that any rule in this class controls online FDR under some standard assumptions. We then focus on a subclass of these procedures, based on weighting significance levels, to derive a practical algorithm that learns a parametric weight function in an online fashion to gain more discoveries. We also theoretically prove, in a stylized setting, that our proposed procedures would lead to an increase in the achieved statistical power over a popular online testing procedure proposed by Javanmard & Montanari (2018). Finally, we demonstrate the favorable performance of our procedure, by comparing it to state-of-the-art online multiple testing procedures, on both synthetic data and real data generated from different applications.

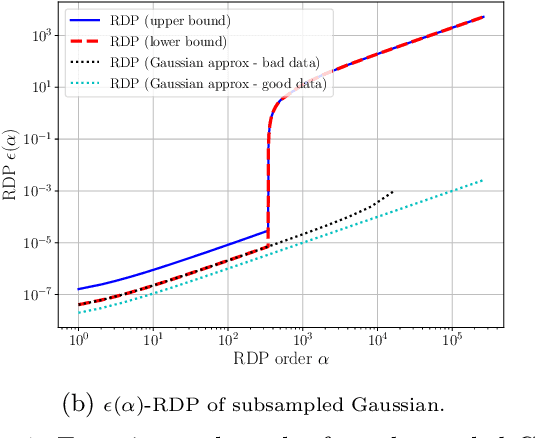
Subsampled Rényi Differential Privacy and Analytical Moments Accountant

We study the problem of subsampling in differential privacy (DP), a question that is the centerpiece behind many successful differentially private machine learning algorithms. Specifically, we provide a tight upper bound on the R\'enyi Differential Privacy (RDP) (Mironov, 2017) parameters for algorithms that: (1) subsample the dataset, and then (2) apply a randomized mechanism M to the subsample, in terms of the RDP parameters of M and the subsampling probability parameter. This result generalizes the classic subsampling-based "privacy amplification" property of $(\epsilon,\delta)$-differential privacy that applies to only one fixed pair of $(\epsilon,\delta)$, to a stronger version that exploits properties of each specific randomized algorithm and satisfies an entire family of $(\epsilon(\delta),\delta)$-differential privacy for all $\delta\in [0,1]$. Our experiments confirm the advantage of using our techniques over keeping track of $(\epsilon,\delta)$ directly, especially in the setting where we need to compose many rounds of data access.

Efficient and Practical Stochastic Subgradient Descent for Nuclear Norm Regularization

We describe novel subgradient methods for a broad class of matrix optimization problems involving nuclear norm regularization. Unlike existing approaches, our method executes very cheap iterations by combining low-rank stochastic subgradients with efficient incremental SVD updates, made possible by highly optimized and parallelizable dense linear algebra operations on small matrices. Our practical algorithms always maintain a low-rank factorization of iterates that can be conveniently held in memory and efficiently multiplied to generate predictions in matrix completion settings. Empirical comparisons confirm that our approach is highly competitive with several recently proposed state-of-the-art solvers for such problems.