AutoMV: An Automatic Multi-Agent System for Music Video Generation

Music-to-Video (M2V) generation for full-length songs faces significant challenges. Existing methods produce short, disjointed clips, failing to align visuals with musical structure, beats, or lyrics, and lack temporal consistency. We propose AutoMV, a multi-agent system that generates full music videos (MVs) directly from a song. AutoMV first applies music processing tools to extract musical attributes, such as structure, vocal tracks, and time-aligned lyrics, and constructs these features as contextual inputs for following agents. The screenwriter Agent and director Agent then use this information to design short script, define character profiles in a shared external bank, and specify camera instructions. Subsequently, these agents call the image generator for keyframes and different video generators for "story" or "singer" scenes. A Verifier Agent evaluates their output, enabling multi-agent collaboration to produce a coherent longform MV. To evaluate M2V generation, we further propose a benchmark with four high-level categories (Music Content, Technical, Post-production, Art) and twelve ine-grained criteria. This benchmark was applied to compare commercial products, AutoMV, and human-directed MVs with expert human raters: AutoMV outperforms current baselines significantly across all four categories, narrowing the gap to professional MVs. Finally, we investigate using large multimodal models as automatic MV judges; while promising, they still lag behind human expert, highlighting room for future work.

Diff4MMLiTS: Advanced Multimodal Liver Tumor Segmentation via Diffusion-Based Image Synthesis and Alignment

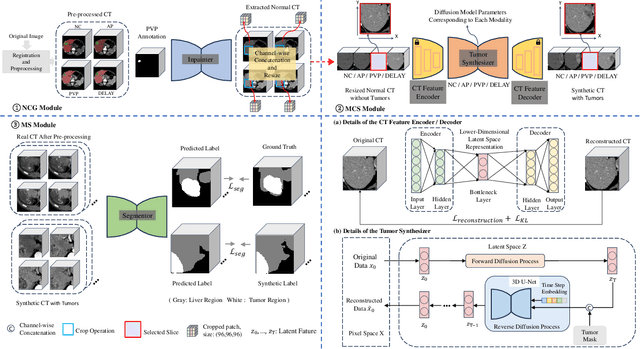
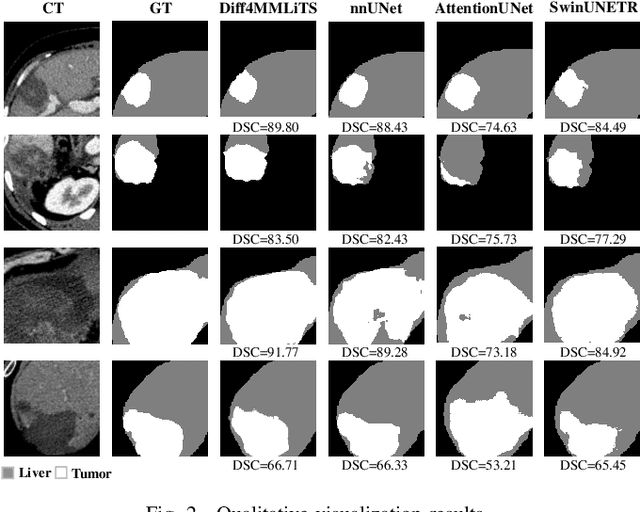
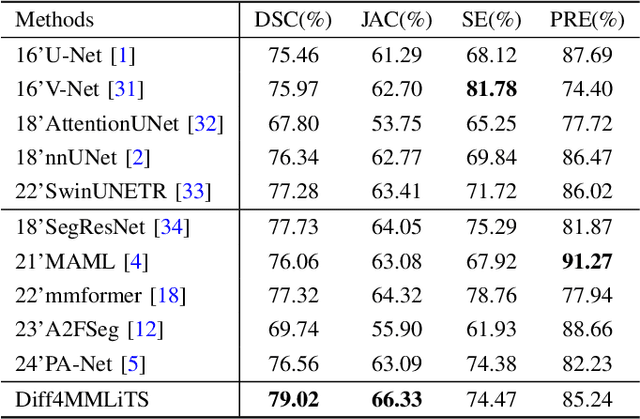
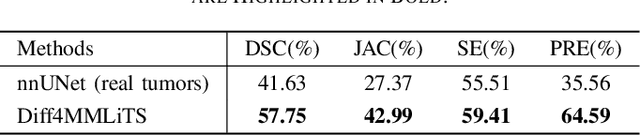
Multimodal learning has been demonstrated to enhance performance across various clinical tasks, owing to the diverse perspectives offered by different modalities of data. However, existing multimodal segmentation methods rely on well-registered multimodal data, which is unrealistic for real-world clinical images, particularly for indistinct and diffuse regions such as liver tumors. In this paper, we introduce Diff4MMLiTS, a four-stage multimodal liver tumor segmentation pipeline: pre-registration of the target organs in multimodal CTs; dilation of the annotated modality's mask and followed by its use in inpainting to obtain multimodal normal CTs without tumors; synthesis of strictly aligned multimodal CTs with tumors using the latent diffusion model based on multimodal CT features and randomly generated tumor masks; and finally, training the segmentation model, thus eliminating the need for strictly aligned multimodal data. Extensive experiments on public and internal datasets demonstrate the superiority of Diff4MMLiTS over other state-of-the-art multimodal segmentation methods.

ASLseg: Adapting SAM in the Loop for Semi-supervised Liver Tumor Segmentation

Liver tumor segmentation is essential for computer-aided diagnosis, surgical planning, and prognosis evaluation. However, obtaining and maintaining a large-scale dataset with dense annotations is challenging. Semi-Supervised Learning (SSL) is a common technique to address these challenges. Recently, Segment Anything Model (SAM) has shown promising performance in some medical image segmentation tasks, but it performs poorly for liver tumor segmentation. In this paper, we propose a novel semi-supervised framework, named ASLseg, which can effectively adapt the SAM to the SSL setting and combine both domain-specific and general knowledge of liver tumors. Specifically, the segmentation model trained with a specific SSL paradigm provides the generated pseudo-labels as prompts to the fine-tuned SAM. An adaptation network is then used to refine the SAM-predictions and generate higher-quality pseudo-labels. Finally, the reliable pseudo-labels are selected to expand the labeled set for iterative training. Extensive experiments on the LiTS dataset demonstrate overwhelming performance of our ASLseg.

Contextual Online False Discovery Rate Control

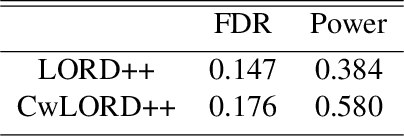
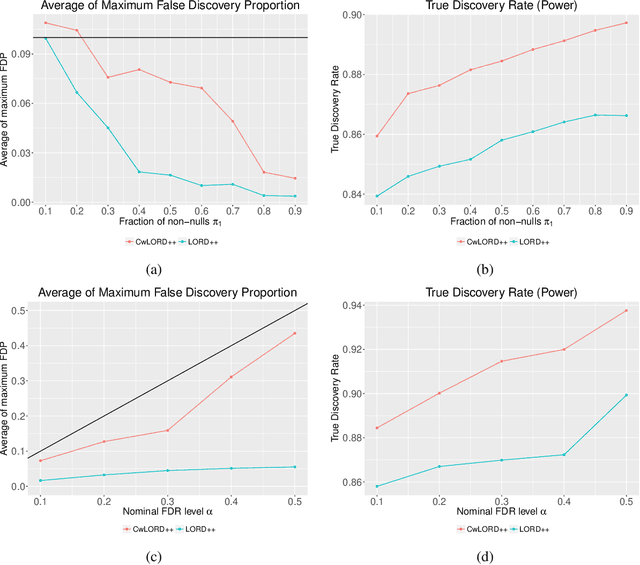
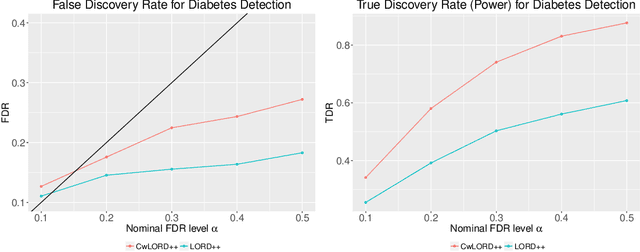
Multiple hypothesis testing, a situation when we wish to consider many hypotheses, is a core problem in statistical inference that arises in almost every scientific field. In this setting, controlling the false discovery rate (FDR), which is the expected proportion of type I error, is an important challenge for making meaningful inferences. In this paper, we consider the problem of controlling FDR in an online manner. Concretely, we consider an ordered, possibly infinite, sequence of hypotheses, arriving one at each timestep, and for each hypothesis we observe a p-value along with a set of features specific to that hypothesis. The decision whether or not to reject the current hypothesis must be made immediately at each timestep, before the next hypothesis is observed. The model of multi-dimensional feature set provides a very general way of leveraging the auxiliary information in the data which helps in maximizing the number of discoveries. We propose a new class of powerful online testing procedures, where the rejections thresholds (significance levels) are learnt sequentially by incorporating contextual information and previous results. We prove that any rule in this class controls online FDR under some standard assumptions. We then focus on a subclass of these procedures, based on weighting significance levels, to derive a practical algorithm that learns a parametric weight function in an online fashion to gain more discoveries. We also theoretically prove, in a stylized setting, that our proposed procedures would lead to an increase in the achieved statistical power over a popular online testing procedure proposed by Javanmard & Montanari (2018). Finally, we demonstrate the favorable performance of our procedure, by comparing it to state-of-the-art online multiple testing procedures, on both synthetic data and real data generated from different applications.