Removing Spurious Correlation from Neural Network Interpretations

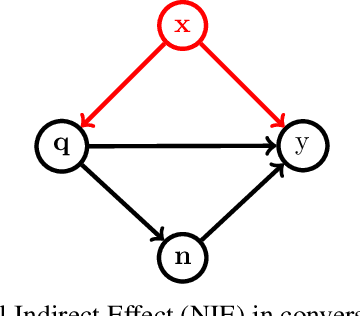
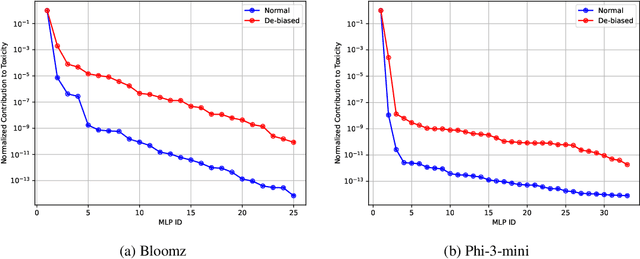
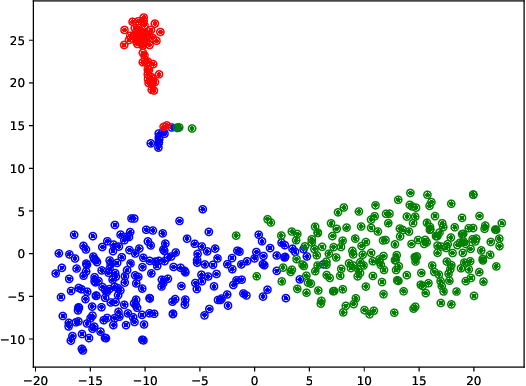
The existing algorithms for identification of neurons responsible for undesired and harmful behaviors do not consider the effects of confounders such as topic of the conversation. In this work, we show that confounders can create spurious correlations and propose a new causal mediation approach that controls the impact of the topic. In experiments with two large language models, we study the localization hypothesis and show that adjusting for the effect of conversation topic, toxicity becomes less localized.

Fast Training Dataset Attribution via In-Context Learning

We investigate the use of in-context learning and prompt engineering to estimate the contributions of training data in the outputs of instruction-tuned large language models (LLMs). We propose two novel approaches: (1) a similarity-based approach that measures the difference between LLM outputs with and without provided context, and (2) a mixture distribution model approach that frames the problem of identifying contribution scores as a matrix factorization task. Our empirical comparison demonstrates that the mixture model approach is more robust to retrieval noise in in-context learning, providing a more reliable estimation of data contributions.

Multiply-Robust Causal Change Attribution

Comparing two samples of data, we observe a change in the distribution of an outcome variable. In the presence of multiple explanatory variables, how much of the change can be explained by each possible cause? We develop a new estimation strategy that, given a causal model, combines regression and re-weighting methods to quantify the contribution of each causal mechanism. Our proposed methodology is multiply robust, meaning that it still recovers the target parameter under partial misspecification. We prove that our estimator is consistent and asymptotically normal. Moreover, it can be incorporated into existing frameworks for causal attribution, such as Shapley values, which will inherit the consistency and large-sample distribution properties. Our method demonstrates excellent performance in Monte Carlo simulations, and we show its usefulness in an empirical application.

Heckerthoughts

This manuscript is technical memoir about my work at Stanford and Microsoft Research. Included are fundamental concepts central to machine learning and artificial intelligence, applications of these concepts, and stories behind their creation.

Likelihoods and Parameter Priors for Bayesian Networks

We develop simple methods for constructing likelihoods and parameter priors for learning about the parameters and structure of a Bayesian network. In particular, we introduce several assumptions that permit the construction of likelihoods and parameter priors for a large number of Bayesian-network structures from a small set of assessments. The most notable assumption is that of likelihood equivalence, which says that data can not help to discriminate network structures that encode the same assertions of conditional independence. We describe the constructions that follow from these assumptions, and also present a method for directly computing the marginal likelihood of a random sample with no missing observations. Also, we show how these assumptions lead to a general framework for characterizing parameter priors of multivariate distributions.

Parameter Priors for Directed Acyclic Graphical Models and the Characterization of Several Probability Distributions

We develop simple methods for constructing parameter priors for model choice among Directed Acyclic Graphical (DAG) models. In particular, we introduce several assumptions that permit the construction of parameter priors for a large number of DAG models from a small set of assessments. We then present a method for directly computing the marginal likelihood of every DAG model given a random sample with no missing observations. We apply this methodology to Gaussian DAG models which consist of a recursive set of linear regression models. We show that the only parameter prior for complete Gaussian DAG models that satisfies our assumptions is the normal-Wishart distribution. Our analysis is based on the following new characterization of the Wishart distribution: let $W$ be an $n \times n$, $n \ge 3$, positive-definite symmetric matrix of random variables and $f(W)$ be a pdf of $W$. Then, f$(W)$ is a Wishart distribution if and only if $W_{11} - W_{12} W_{22}^{-1} W'_{12}$ is independent of $\{W_{12},W_{22}\}$ for every block partitioning $W_{11},W_{12}, W'_{12}, W_{22}$ of $W$. Similar characterizations of the normal and normal-Wishart distributions are provided as well.

A Tutorial on Learning With Bayesian Networks

A Bayesian network is a graphical model that encodes probabilistic relationships among variables of interest. When used in conjunction with statistical techniques, the graphical model has several advantages for data analysis. One, because the model encodes dependencies among all variables, it readily handles situations where some data entries are missing. Two, a Bayesian network can be used to learn causal relationships, and hence can be used to gain understanding about a problem domain and to predict the consequences of intervention. Three, because the model has both a causal and probabilistic semantics, it is an ideal representation for combining prior knowledge (which often comes in causal form) and data. Four, Bayesian statistical methods in conjunction with Bayesian networks offer an efficient and principled approach for avoiding the overfitting of data. In this paper, we discuss methods for constructing Bayesian networks from prior knowledge and summarize Bayesian statistical methods for using data to improve these models. With regard to the latter task, we describe methods for learning both the parameters and structure of a Bayesian network, including techniques for learning with incomplete data. In addition, we relate Bayesian-network methods for learning to techniques for supervised and unsupervised learning. We illustrate the graphical-modeling approach using a real-world case study.

Probabilistic Similarity Networks

Normative expert systems have not become commonplace because they have been difficult to build and use. Over the past decade, however, researchers have developed the influence diagram, a graphical representation of a decision maker's beliefs, alternatives, and preferences that serves as the knowledge base of a normative expert system. Most people who have seen the representation find it intuitive and easy to use. Consequently, the influence diagram has overcome significantly the barriers to constructing normative expert systems. Nevertheless, building influence diagrams is not practical for extremely large and complex domains. In this book, I address the difficulties associated with the construction of the probabilistic portion of an influence diagram, called a knowledge map, belief network, or Bayesian network. I introduce two representations that facilitate the generation of large knowledge maps. In particular, I introduce the similarity network, a tool for building the network structure of a knowledge map, and the partition, a tool for assessing the probabilities associated with a knowledge map. I then use these representations to build Pathfinder, a large normative expert system for the diagnosis of lymph-node diseases (the domain contains over 60 diseases and over 100 disease findings). In an early version of the system, I encoded the knowledge of the expert using an erroneous assumption that all disease findings were independent, given each disease. When the expert and I attempted to build a more accurate knowledge map for the domain that would capture the dependencies among the disease findings, we failed. Using a similarity network, however, we built the knowledge-map structure for the entire domain in approximately 40 hours. Furthermore, the partition representation reduced the number of probability assessments required by the expert from 75,000 to 14,000.

Embedded Bayesian Network Classifiers

Low-dimensional probability models for local distribution functions in a Bayesian network include decision trees, decision graphs, and causal independence models. We describe a new probability model for discrete Bayesian networks, which we call an embedded Bayesian network classifier or EBNC. The model for a node $Y$ given parents $\bf X$ is obtained from a (usually different) Bayesian network for $Y$ and $\bf X$ in which $\bf X$ need not be the parents of $Y$. We show that an EBNC is a special case of a softmax polynomial regression model. Also, we show how to identify a non-redundant set of parameters for an EBNC, and describe an asymptotic approximation for learning the structure of Bayesian networks that contain EBNCs. Unlike the decision tree, decision graph, and causal independence models, we are unaware of a semantic justification for the use of these models. Experiments are needed to determine whether the models presented in this paper are useful in practice.

Accounting for hidden common causes when inferring cause and effect from observational data

Identifying causal relationships from observation data is difficult, in large part, due to the presence of hidden common causes. In some cases, where just the right patterns of conditional independence and dependence lie in the data---for example, Y-structures---it is possible to identify cause and effect. In other cases, the analyst deliberately makes an uncertain assumption that hidden common causes are absent, and infers putative causal relationships to be tested in a randomized trial. Here, we consider a third approach, where there are sufficient clues in the data such that hidden common causes can be inferred.