Likelihoods and Parameter Priors for Bayesian Networks

We develop simple methods for constructing likelihoods and parameter priors for learning about the parameters and structure of a Bayesian network. In particular, we introduce several assumptions that permit the construction of likelihoods and parameter priors for a large number of Bayesian-network structures from a small set of assessments. The most notable assumption is that of likelihood equivalence, which says that data can not help to discriminate network structures that encode the same assertions of conditional independence. We describe the constructions that follow from these assumptions, and also present a method for directly computing the marginal likelihood of a random sample with no missing observations. Also, we show how these assumptions lead to a general framework for characterizing parameter priors of multivariate distributions.

Parameter Priors for Directed Acyclic Graphical Models and the Characterization of Several Probability Distributions

We develop simple methods for constructing parameter priors for model choice among Directed Acyclic Graphical (DAG) models. In particular, we introduce several assumptions that permit the construction of parameter priors for a large number of DAG models from a small set of assessments. We then present a method for directly computing the marginal likelihood of every DAG model given a random sample with no missing observations. We apply this methodology to Gaussian DAG models which consist of a recursive set of linear regression models. We show that the only parameter prior for complete Gaussian DAG models that satisfies our assumptions is the normal-Wishart distribution. Our analysis is based on the following new characterization of the Wishart distribution: let $W$ be an $n \times n$, $n \ge 3$, positive-definite symmetric matrix of random variables and $f(W)$ be a pdf of $W$. Then, f$(W)$ is a Wishart distribution if and only if $W_{11} - W_{12} W_{22}^{-1} W'_{12}$ is independent of $\{W_{12},W_{22}\}$ for every block partitioning $W_{11},W_{12}, W'_{12}, W_{22}$ of $W$. Similar characterizations of the normal and normal-Wishart distributions are provided as well.

Dependence and Relevance: A probabilistic view

We examine three probabilistic concepts related to the sentence "two variables have no bearing on each other". We explore the relationships between these three concepts and establish their relevance to the process of constructing similarity networks---a tool for acquiring probabilistic knowledge from human experts. We also establish a precise relationship between connectedness in Bayesian networks and relevance in probability.

Separable and transitive graphoids

We examine three probabilistic formulations of the sentence a and b are totally unrelated with respect to a given set of variables U. First, two variables a and b are totally independent if they are independent given any value of any subset of the variables in U. Second, two variables are totally uncoupled if U can be partitioned into two marginally independent sets containing a and b respectively. Third, two variables are totally disconnected if the corresponding nodes are disconnected in every belief network representation. We explore the relationship between these three formulations of unrelatedness and explain their relevance to the process of acquiring probabilistic knowledge from human experts.

Advances in Probabilistic Reasoning

This paper discuses multiple Bayesian networks representation paradigms for encoding asymmetric independence assertions. We offer three contributions: (1) an inference mechanism that makes explicit use of asymmetric independence to speed up computations, (2) a simplified definition of similarity networks and extensions of their theory, and (3) a generalized representation scheme that encodes more types of asymmetric independence assertions than do similarity networks.

Inference Algorithms for Similarity Networks

We examine two types of similarity networks each based on a distinct notion of relevance. For both types of similarity networks we present an efficient inference algorithm that works under the assumption that every event has a nonzero probability of occurrence. Another inference algorithm is developed for type 1 similarity networks that works under no restriction, albeit less efficiently.

Learning Bayesian Networks: The Combination of Knowledge and Statistical Data

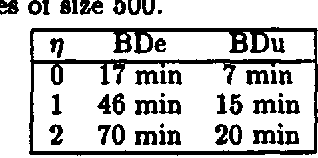
We describe algorithms for learning Bayesian networks from a combination of user knowledge and statistical data. The algorithms have two components: a scoring metric and a search procedure. The scoring metric takes a network structure, statistical data, and a user's prior knowledge, and returns a score proportional to the posterior probability of the network structure given the data. The search procedure generates networks for evaluation by the scoring metric. Our contributions are threefold. First, we identify two important properties of metrics, which we call event equivalence and parameter modularity. These properties have been mostly ignored, but when combined, greatly simplify the encoding of a user's prior knowledge. In particular, a user can express her knowledge-for the most part-as a single prior Bayesian network for the domain. Second, we describe local search and annealing algorithms to be used in conjunction with scoring metrics. In the special case where each node has at most one parent, we show that heuristic search can be replaced with a polynomial algorithm to identify the networks with the highest score. Third, we describe a methodology for evaluating Bayesian-network learning algorithms. We apply this approach to a comparison of metrics and search procedures.

Asymptotic Model Selection for Directed Networks with Hidden Variables

We extend the Bayesian Information Criterion (BIC), an asymptotic approximation for the marginal likelihood, to Bayesian networks with hidden variables. This approximation can be used to select models given large samples of data. The standard BIC as well as our extension punishes the complexity of a model according to the dimension of its parameters. We argue that the dimension of a Bayesian network with hidden variables is the rank of the Jacobian matrix of the transformation between the parameters of the network and the parameters of the observable variables. We compute the dimensions of several networks including the naive Bayes model with a hidden root node.

Random Algorithms for the Loop Cutset Problem

We show how to find a minimum loop cutset in a Bayesian network with high probability. Finding such a loop cutset is the first step in Pearl's method of conditioning for inference. Our random algorithm for finding a loop cutset, called "Repeated WGuessI", outputs a minimum loop cutset, after O(c 6^k k n) steps, with probability at least 1-(1 over{6^k})^{c 6^k}), where c>1 is a constant specified by the user, k is the size of a minimum weight loop cutset, and n is the number of vertices. We also show empirically that a variant of this algorithm, called WRA, often finds a loop cutset that is closer to the minimum loop cutset than the ones found by the best deterministic algorithms known.

Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence (1997)

This is the Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence, which was held in Providence, RI, August 1-3, 1997