Selective Greedy Equivalence Search: Finding Optimal Bayesian Networks Using a Polynomial Number of Score Evaluations

We introduce Selective Greedy Equivalence Search (SGES), a restricted version of Greedy Equivalence Search (GES). SGES retains the asymptotic correctness of GES but, unlike GES, has polynomial performance guarantees. In particular, we show that when data are sampled independently from a distribution that is perfect with respect to a DAG ${\cal G}$ defined over the observable variables then, in the limit of large data, SGES will identify ${\cal G}$'s equivalence class after a number of score evaluations that is (1) polynomial in the number of nodes and (2) exponential in various complexity measures including maximum-number-of-parents, maximum-clique-size, and a new measure called {\em v-width} that is at least as small as---and potentially much smaller than---the other two. More generally, we show that for any hereditary and equivalence-invariant property $\Pi$ known to hold in ${\cal G}$, we retain the large-sample optimality guarantees of GES even if we ignore any GES deletion operator during the backward phase that results in a state for which $\Pi$ does not hold in the common-descendants subgraph.

Efficient Approximations for the Marginal Likelihood of Incomplete Data Given a Bayesian Network

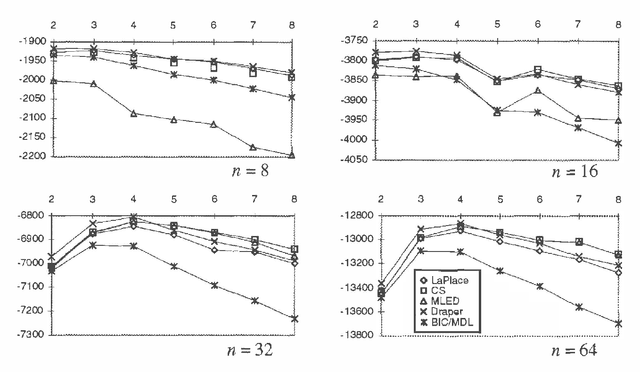
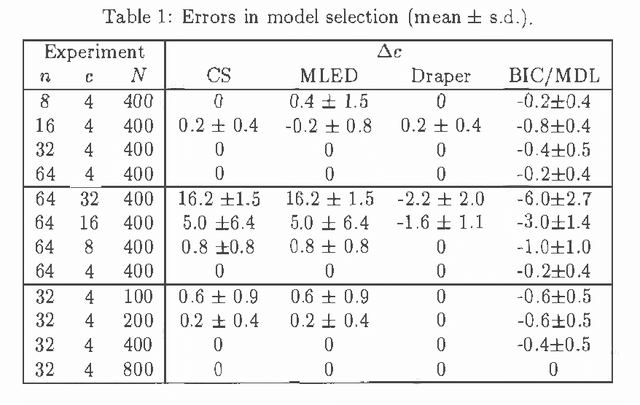
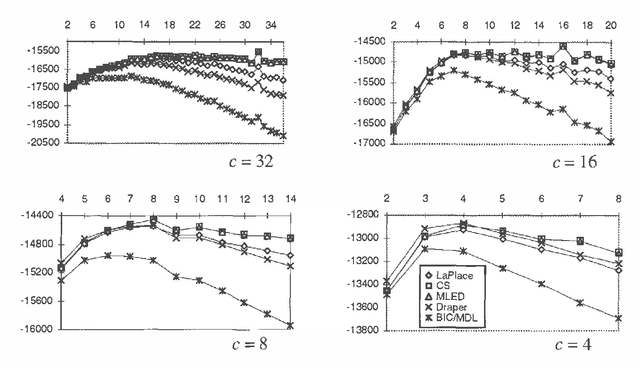
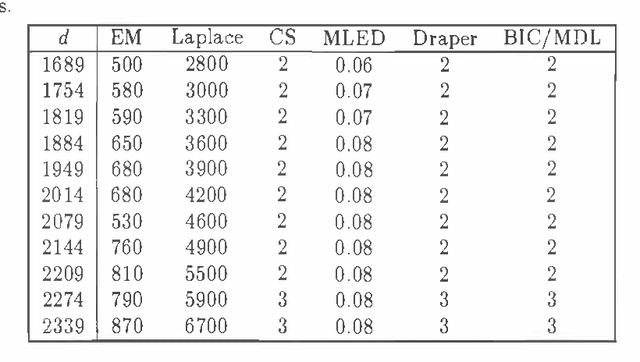
We discuss Bayesian methods for learning Bayesian networks when data sets are incomplete. In particular, we examine asymptotic approximations for the marginal likelihood of incomplete data given a Bayesian network. We consider the Laplace approximation and the less accurate but more efficient BIC/MDL approximation. We also consider approximations proposed by Draper (1993) and Cheeseman and Stutz (1995). These approximations are as efficient as BIC/MDL, but their accuracy has not been studied in any depth. We compare the accuracy of these approximations under the assumption that the Laplace approximation is the most accurate. In experiments using synthetic data generated from discrete naive-Bayes models having a hidden root node, we find that the CS measure is the most accurate.

Learning Bayesian Networks: The Combination of Knowledge and Statistical Data

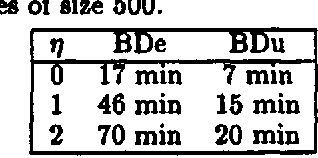
We describe algorithms for learning Bayesian networks from a combination of user knowledge and statistical data. The algorithms have two components: a scoring metric and a search procedure. The scoring metric takes a network structure, statistical data, and a user's prior knowledge, and returns a score proportional to the posterior probability of the network structure given the data. The search procedure generates networks for evaluation by the scoring metric. Our contributions are threefold. First, we identify two important properties of metrics, which we call event equivalence and parameter modularity. These properties have been mostly ignored, but when combined, greatly simplify the encoding of a user's prior knowledge. In particular, a user can express her knowledge-for the most part-as a single prior Bayesian network for the domain. Second, we describe local search and annealing algorithms to be used in conjunction with scoring metrics. In the special case where each node has at most one parent, we show that heuristic search can be replaced with a polynomial algorithm to identify the networks with the highest score. Third, we describe a methodology for evaluating Bayesian-network learning algorithms. We apply this approach to a comparison of metrics and search procedures.

A Bayesian Approach to Learning Bayesian Networks with Local Structure

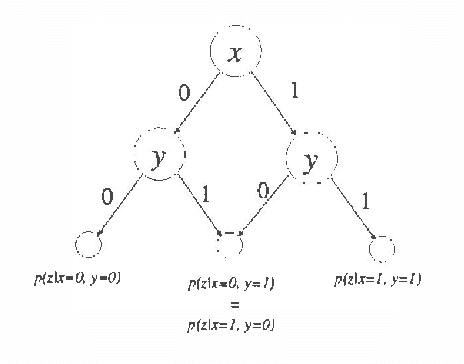
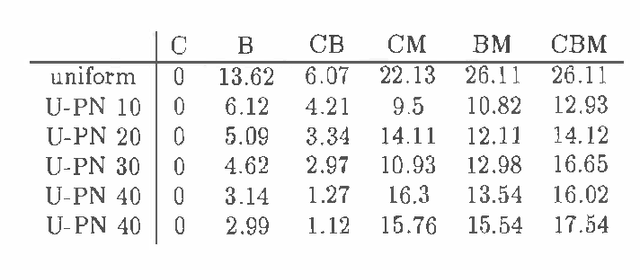
Recently several researchers have investigated techniques for using data to learn Bayesian networks containing compact representations for the conditional probability distributions (CPDs) stored at each node. The majority of this work has concentrated on using decision-tree representations for the CPDs. In addition, researchers typically apply non-Bayesian (or asymptotically Bayesian) scoring functions such as MDL to evaluate the goodness-of-fit of networks to the data. In this paper we investigate a Bayesian approach to learning Bayesian networks that contain the more general decision-graph representations of the CPDs. First, we describe how to evaluate the posterior probability that is, the Bayesian score of such a network, given a database of observed cases. Second, we describe various search spaces that can be used, in conjunction with a scoring function and a search procedure, to identify one or more high-scoring networks. Finally, we present an experimental evaluation of the search spaces, using a greedy algorithm and a Bayesian scoring function.

Learning Mixtures of DAG Models

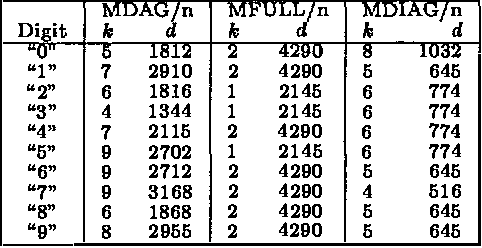
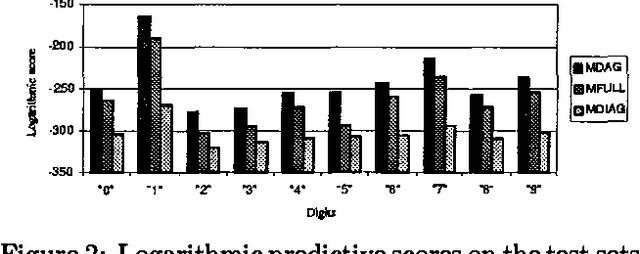
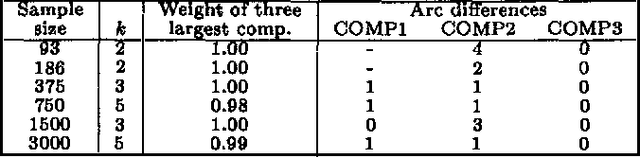
We describe computationally efficient methods for learning mixtures in which each component is a directed acyclic graphical model (mixtures of DAGs or MDAGs). We argue that simple search-and-score algorithms are infeasible for a variety of problems, and introduce a feasible approach in which parameter and structure search is interleaved and expected data is treated as real data. Our approach can be viewed as a combination of (1) the Cheeseman--Stutz asymptotic approximation for model posterior probability and (2) the Expectation--Maximization algorithm. We evaluate our procedure for selecting among MDAGs on synthetic and real examples.

Fast Learning from Sparse Data

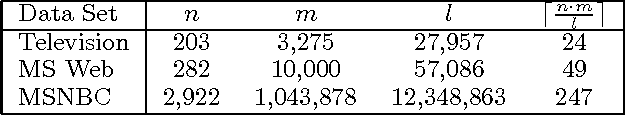
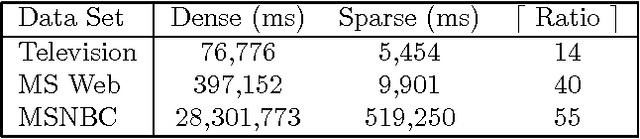
We describe two techniques that significantly improve the running time of several standard machine-learning algorithms when data is sparse. The first technique is an algorithm that effeciently extracts one-way and two-way counts--either real or expected-- from discrete data. Extracting such counts is a fundamental step in learning algorithms for constructing a variety of models including decision trees, decision graphs, Bayesian networks, and naive-Bayes clustering models. The second technique is an algorithm that efficiently performs the E-step of the EM algorithm (i.e. inference) when applied to a naive-Bayes clustering model. Using real-world data sets, we demonstrate a dramatic decrease in running time for algorithms that incorporate these techniques.

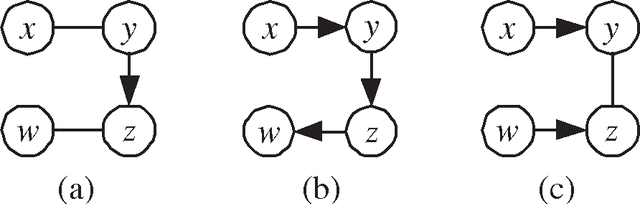
A Transformational Characterization of Equivalent Bayesian Network Structures

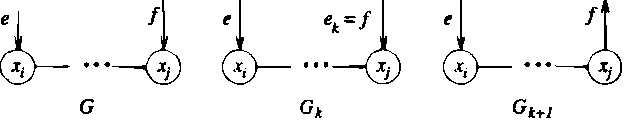
We present a simple characterization of equivalent Bayesian network structures based on local transformations. The significance of the characterization is twofold. First, we are able to easily prove several new invariant properties of theoretical interest for equivalent structures. Second, we use the characterization to derive an efficient algorithm that identifies all of the compelled edges in a structure. Compelled edge identification is of particular importance for learning Bayesian network structures from data because these edges indicate causal relationships when certain assumptions hold.

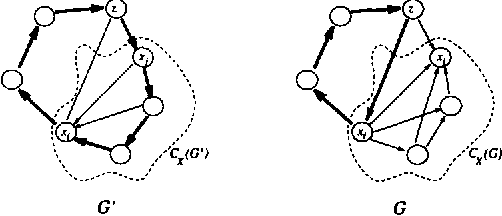
Learning Equivalence Classes of Bayesian Networks Structures

Approaches to learning Bayesian networks from data typically combine a scoring function with a heuristic search procedure. Given a Bayesian network structure, many of the scoring functions derived in the literature return a score for the entire equivalence class to which the structure belongs. When using such a scoring function, it is appropriate for the heuristic search algorithm to search over equivalence classes of Bayesian networks as opposed to individual structures. We present the general formulation of a search space for which the states of the search correspond to equivalence classes of structures. Using this space, any one of a number of heuristic search algorithms can easily be applied. We compare greedy search performance in the proposed search space to greedy search performance in a search space for which the states correspond to individual Bayesian network structures.

Dependency Networks for Collaborative Filtering and Data Visualization

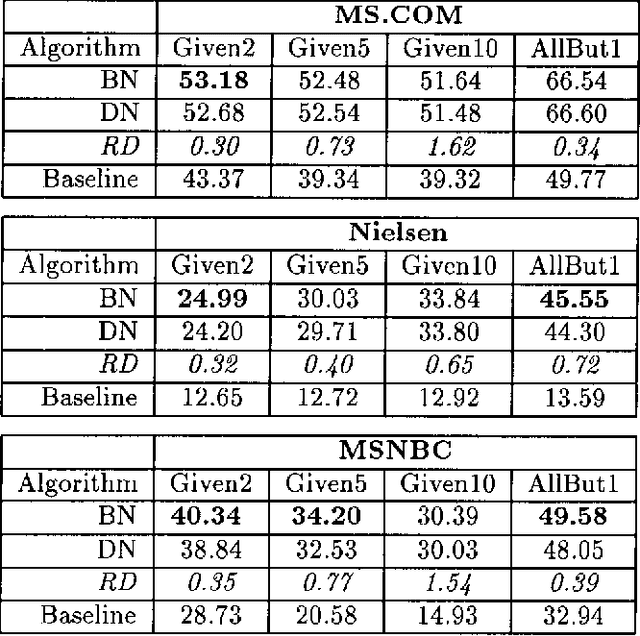
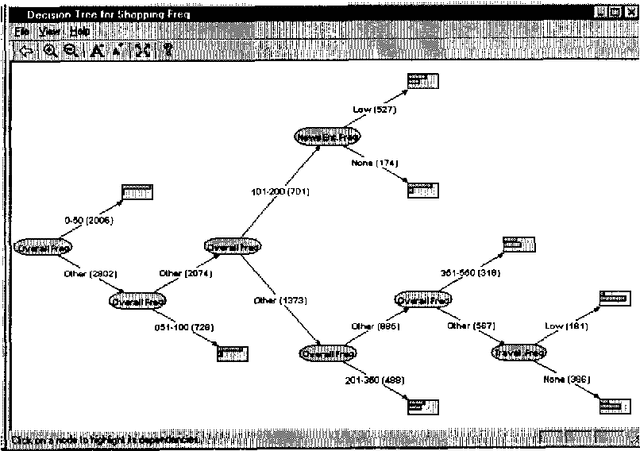
We describe a graphical model for probabilistic relationships---an alternative to the Bayesian network---called a dependency network. The graph of a dependency network, unlike a Bayesian network, is potentially cyclic. The probability component of a dependency network, like a Bayesian network, is a set of conditional distributions, one for each node given its parents. We identify several basic properties of this representation and describe a computationally efficient procedure for learning the graph and probability components from data. We describe the application of this representation to probabilistic inference, collaborative filtering (the task of predicting preferences), and the visualization of acausal predictive relationships.

A Decision Theoretic Approach to Targeted Advertising

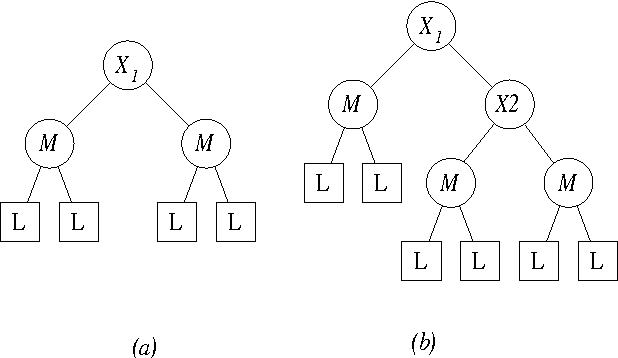
A simple advertising strategy that can be used to help increase sales of a product is to mail out special offers to selected potential customers. Because there is a cost associated with sending each offer, the optimal mailing strategy depends on both the benefit obtained from a purchase and how the offer affects the buying behavior of the customers. In this paper, we describe two methods for partitioning the potential customers into groups, and show how to perform a simple cost-benefit analysis to decide which, if any, of the groups should be targeted. In particular, we consider two decision-tree learning algorithms. The first is an "off the shelf" algorithm used to model the probability that groups of customers will buy the product. The second is a new algorithm that is similar to the first, except that for each group, it explicitly models the probability of purchase under the two mailing scenarios: (1) the mail is sent to members of that group and (2) the mail is not sent to members of that group. Using data from a real-world advertising experiment, we compare the algorithms to each other and to a naive mail-to-all strategy.