A Bayesian Approach to Learning Bayesian Networks with Local Structure
Paper and Code
May 16, 2015

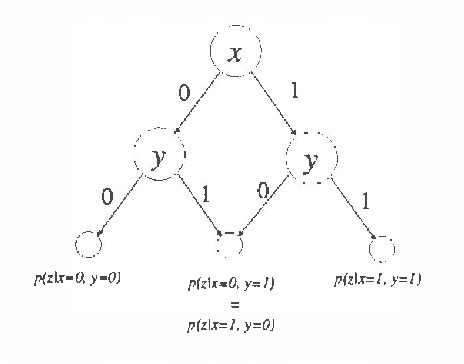
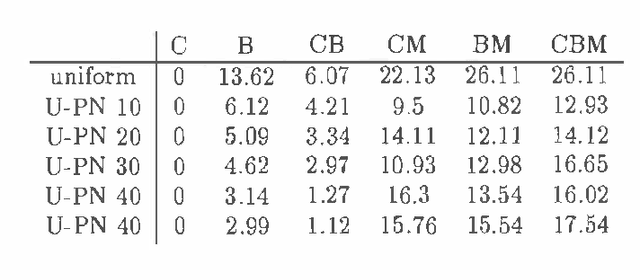
Recently several researchers have investigated techniques for using data to learn Bayesian networks containing compact representations for the conditional probability distributions (CPDs) stored at each node. The majority of this work has concentrated on using decision-tree representations for the CPDs. In addition, researchers typically apply non-Bayesian (or asymptotically Bayesian) scoring functions such as MDL to evaluate the goodness-of-fit of networks to the data. In this paper we investigate a Bayesian approach to learning Bayesian networks that contain the more general decision-graph representations of the CPDs. First, we describe how to evaluate the posterior probability that is, the Bayesian score of such a network, given a database of observed cases. Second, we describe various search spaces that can be used, in conjunction with a scoring function and a search procedure, to identify one or more high-scoring networks. Finally, we present an experimental evaluation of the search spaces, using a greedy algorithm and a Bayesian scoring function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge