Learning Mixtures of DAG Models
Paper and Code
May 16, 2015
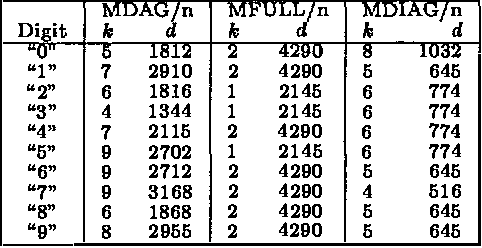
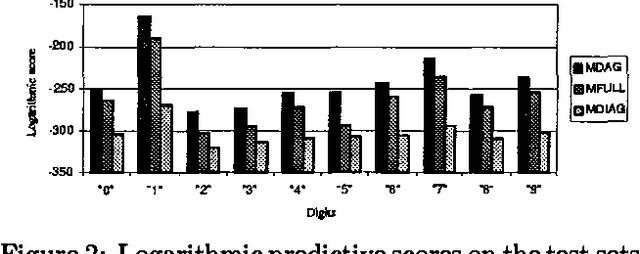
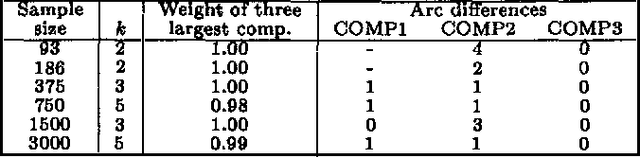
We describe computationally efficient methods for learning mixtures in which each component is a directed acyclic graphical model (mixtures of DAGs or MDAGs). We argue that simple search-and-score algorithms are infeasible for a variety of problems, and introduce a feasible approach in which parameter and structure search is interleaved and expected data is treated as real data. Our approach can be viewed as a combination of (1) the Cheeseman--Stutz asymptotic approximation for model posterior probability and (2) the Expectation--Maximization algorithm. We evaluate our procedure for selecting among MDAGs on synthetic and real examples.
* Appears in Proceedings of the Fourteenth Conference on Uncertainty in
Artificial Intelligence (UAI1998)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge