A Transformational Characterization of Equivalent Bayesian Network Structures
Paper and Code
Feb 20, 2013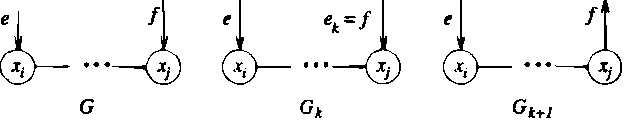

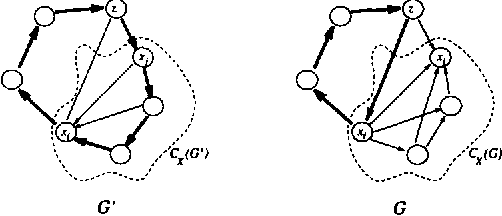

We present a simple characterization of equivalent Bayesian network structures based on local transformations. The significance of the characterization is twofold. First, we are able to easily prove several new invariant properties of theoretical interest for equivalent structures. Second, we use the characterization to derive an efficient algorithm that identifies all of the compelled edges in a structure. Compelled edge identification is of particular importance for learning Bayesian network structures from data because these edges indicate causal relationships when certain assumptions hold.
* Appears in Proceedings of the Eleventh Conference on Uncertainty in
Artificial Intelligence (UAI1995)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge