Removing Spurious Correlation from Neural Network Interpretations

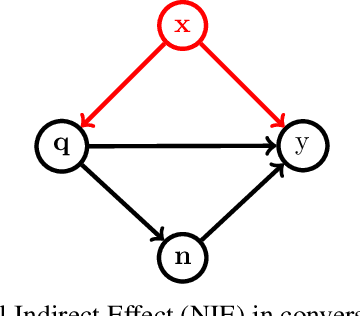
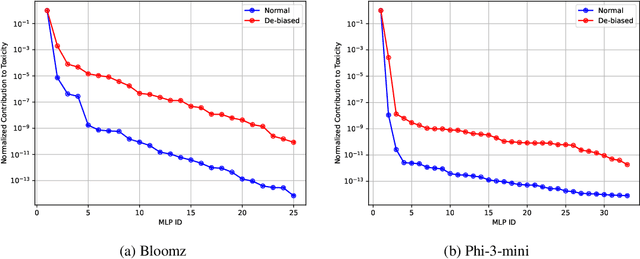
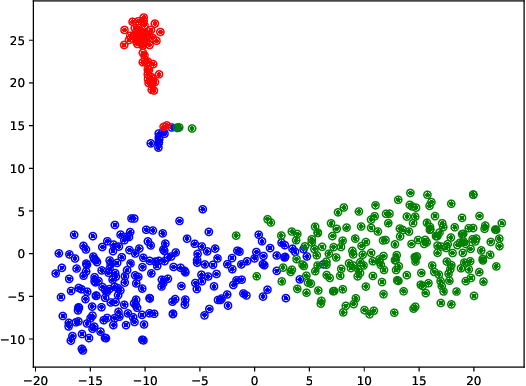
The existing algorithms for identification of neurons responsible for undesired and harmful behaviors do not consider the effects of confounders such as topic of the conversation. In this work, we show that confounders can create spurious correlations and propose a new causal mediation approach that controls the impact of the topic. In experiments with two large language models, we study the localization hypothesis and show that adjusting for the effect of conversation topic, toxicity becomes less localized.

Fast Training Dataset Attribution via In-Context Learning

We investigate the use of in-context learning and prompt engineering to estimate the contributions of training data in the outputs of instruction-tuned large language models (LLMs). We propose two novel approaches: (1) a similarity-based approach that measures the difference between LLM outputs with and without provided context, and (2) a mixture distribution model approach that frames the problem of identifying contribution scores as a matrix factorization task. Our empirical comparison demonstrates that the mixture model approach is more robust to retrieval noise in in-context learning, providing a more reliable estimation of data contributions.

On Codomain Separability and Label Inference from (Noisy) Loss Functions

Machine learning classifiers rely on loss functions for performance evaluation, often on a private (hidden) dataset. Label inference was recently introduced as the problem of reconstructing the ground truth labels of this private dataset from just the (possibly perturbed) loss function values evaluated at chosen prediction vectors, without any other access to the hidden dataset. Existing results have demonstrated this inference is possible on specific loss functions like the cross-entropy loss. In this paper, we introduce the notion of codomain separability to formally study the necessary and sufficient conditions under which label inference is possible from any (noisy) loss function values. Using this notion, we show that for many commonly used loss functions, including multiclass cross-entropy with common activation functions and some Bregman divergence-based losses, it is possible to design label inference attacks for arbitrary noise levels. We demonstrate that these attacks can also be carried out through actual neural network models, and argue, both formally and empirically, the role of finite precision arithmetic in this setting.

Label Inference Attacks from Log-loss Scores

Log-loss (also known as cross-entropy loss) metric is ubiquitously used across machine learning applications to assess the performance of classification algorithms. In this paper, we investigate the problem of inferring the labels of a dataset from single (or multiple) log-loss score(s), without any other access to the dataset. Surprisingly, we show that for any finite number of label classes, it is possible to accurately infer the labels of the dataset from the reported log-loss score of a single carefully constructed prediction vector if we allow arbitrary precision arithmetic. Additionally, we present label inference algorithms (attacks) that succeed even under addition of noise to the log-loss scores and under limited precision arithmetic. All our algorithms rely on ideas from number theory and combinatorics and require no model training. We run experimental simulations on some real datasets to demonstrate the ease of running these attacks in practice.

On a Utilitarian Approach to Privacy Preserving Text Generation

Differentially-private mechanisms for text generation typically add carefully calibrated noise to input words and use the nearest neighbor to the noised input as the output word. When the noise is small in magnitude, these mechanisms are susceptible to reconstruction of the original sensitive text. This is because the nearest neighbor to the noised input is likely to be the original input. To mitigate this empirical privacy risk, we propose a novel class of differentially private mechanisms that parameterizes the nearest neighbor selection criterion in traditional mechanisms. Motivated by Vickrey auction, where only the second highest price is revealed and the highest price is kept private, we balance the choice between the first and the second nearest neighbors in the proposed class of mechanisms using a tuning parameter. This parameter is selected by empirically solving a constrained optimization problem for maximizing utility, while maintaining the desired privacy guarantees. We argue that this empirical measurement framework can be used to align different mechanisms along a common benchmark for their privacy-utility tradeoff, particularly when different distance metrics are used to calibrate the amount of noise added. Our experiments on real text classification datasets show up to 50% improvement in utility compared to the existing state-of-the-art with the same empirical privacy guarantee.

Research Challenges in Designing Differentially Private Text Generation Mechanisms

Accurately learning from user data while ensuring quantifiable privacy guarantees provides an opportunity to build better Machine Learning (ML) models while maintaining user trust. Recent literature has demonstrated the applicability of a generalized form of Differential Privacy to provide guarantees over text queries. Such mechanisms add privacy preserving noise to vectorial representations of text in high dimension and return a text based projection of the noisy vectors. However, these mechanisms are sub-optimal in their trade-off between privacy and utility. This is due to factors such as a fixed global sensitivity which leads to too much noise added in dense spaces while simultaneously guaranteeing protection for sensitive outliers. In this proposal paper, we describe some challenges in balancing the tradeoff between privacy and utility for these differentially private text mechanisms. At a high level, we provide two proposals: (1) a framework called LAC which defers some of the noise to a privacy amplification step and (2), an additional suite of three different techniques for calibrating the noise based on the local region around a word. Our objective in this paper is not to evaluate a single solution but to further the conversation on these challenges and chart pathways for building better mechanisms.

A Differentially Private Text Perturbation Method Using a Regularized Mahalanobis Metric

Balancing the privacy-utility tradeoff is a crucial requirement of many practical machine learning systems that deal with sensitive customer data. A popular approach for privacy-preserving text analysis is noise injection, in which text data is first mapped into a continuous embedding space, perturbed by sampling a spherical noise from an appropriate distribution, and then projected back to the discrete vocabulary space. While this allows the perturbation to admit the required metric differential privacy, often the utility of downstream tasks modeled on this perturbed data is low because the spherical noise does not account for the variability in the density around different words in the embedding space. In particular, words in a sparse region are likely unchanged even when the noise scale is large. %Using the global sensitivity of the mechanism can potentially add too much noise to the words in the dense regions of the embedding space, causing a high utility loss, whereas using local sensitivity can leak information through the scale of the noise added. In this paper, we propose a text perturbation mechanism based on a carefully designed regularized variant of the Mahalanobis metric to overcome this problem. For any given noise scale, this metric adds an elliptical noise to account for the covariance structure in the embedding space. This heterogeneity in the noise scale along different directions helps ensure that the words in the sparse region have sufficient likelihood of replacement without sacrificing the overall utility. We provide a text-perturbation algorithm based on this metric and formally prove its privacy guarantees. Additionally, we empirically show that our mechanism improves the privacy statistics to achieve the same level of utility as compared to the state-of-the-art Laplace mechanism.

Differentially Private Adversarial Robustness Through Randomized Perturbations

Deep Neural Networks, despite their great success in diverse domains, are provably sensitive to small perturbations on correctly classified examples and lead to erroneous predictions. Recently, it was proposed that this behavior can be combatted by optimizing the worst case loss function over all possible substitutions of training examples. However, this can be prone to weighing unlikely substitutions higher, limiting the accuracy gain. In this paper, we study adversarial robustness through randomized perturbations, which has two immediate advantages: (1) by ensuring that substitution likelihood is weighted by the proximity to the original word, we circumvent optimizing the worst case guarantees and achieve performance gains; and (2) the calibrated randomness imparts differentially-private model training, which additionally improves robustness against adversarial attacks on the model outputs. Our approach uses a novel density-based mechanism based on truncated Gumbel noise, which ensures training on substitutions of both rare and dense words in the vocabulary while maintaining semantic similarity for model robustness.

On Primes, Log-Loss Scores and Privacy

Membership Inference Attacks exploit the vulnerabilities of exposing models trained on customer data to queries by an adversary. In a recently proposed implementation of an auditing tool for measuring privacy leakage from sensitive datasets, more refined aggregates like the Log-Loss scores are exposed for simulating inference attacks as well as to assess the total privacy leakage based on the adversary's predictions. In this paper, we prove that this additional information enables the adversary to infer the membership of any number of datapoints with full accuracy in a single query, causing complete membership privacy breach. Our approach obviates any attack model training or access to side knowledge with the adversary. Moreover, our algorithms are agnostic to the model under attack and hence, enable perfect membership inference even for models that do not memorize or overfit. In particular, our observations provide insight into the extent of information leakage from statistical aggregates and how they can be exploited.

Leveraging Hierarchical Representations for Preserving Privacy and Utility in Text

Guaranteeing a certain level of user privacy in an arbitrary piece of text is a challenging issue. However, with this challenge comes the potential of unlocking access to vast data stores for training machine learning models and supporting data driven decisions. We address this problem through the lens of dx-privacy, a generalization of Differential Privacy to non Hamming distance metrics. In this work, we explore word representations in Hyperbolic space as a means of preserving privacy in text. We provide a proof satisfying dx-privacy, then we define a probability distribution in Hyperbolic space and describe a way to sample from it in high dimensions. Privacy is provided by perturbing vector representations of words in high dimensional Hyperbolic space to obtain a semantic generalization. We conduct a series of experiments to demonstrate the tradeoff between privacy and utility. Our privacy experiments illustrate protections against an authorship attribution algorithm while our utility experiments highlight the minimal impact of our perturbations on several downstream machine learning models. Compared to the Euclidean baseline, we observe > 20x greater guarantees on expected privacy against comparable worst case statistics.