Exploring Simple Triangular and Hexagonal Grid Polygons Online

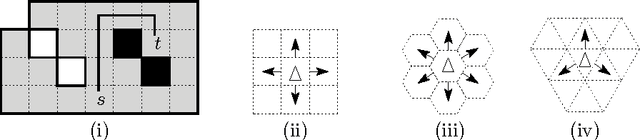
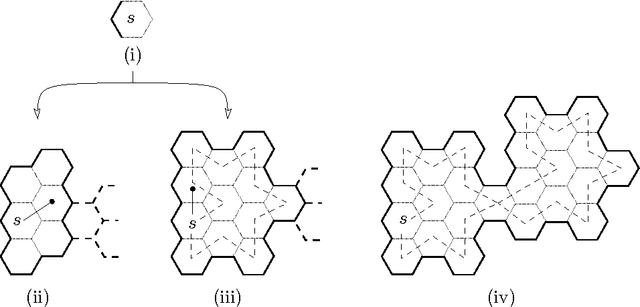
We investigate the online exploration problem (aka covering) of a short-sighted mobile robot moving in an unknown cellular environment with hexagons and triangles as types of cells. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 3 or 6 adjacent cells exist and which are boundary edges. The robot's task is to visit every cell in the given environment and to return to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For arbitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/4 E - 2.5 for hexagonal grids, and S <= C + E - 4 for triangular grids. C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-of the given environment. Further, we show that our strategy is 4/3-competitive in both types of grids, and we provide lower bounds of 14/13 for hexagonal grids and 7/6 for triangular grids.

Exploring Grid Polygons Online

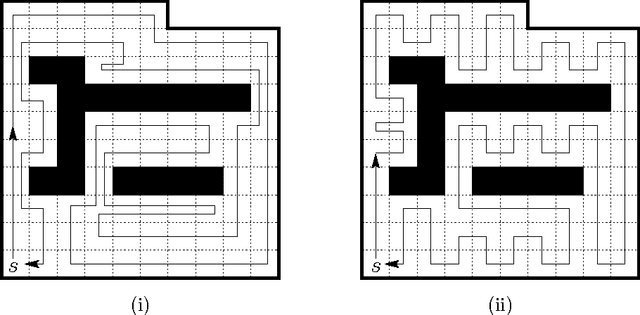
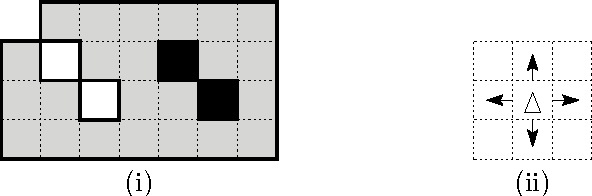
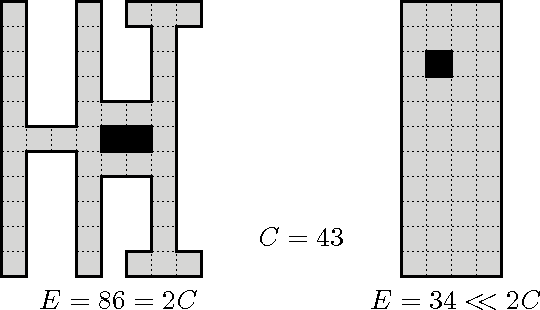
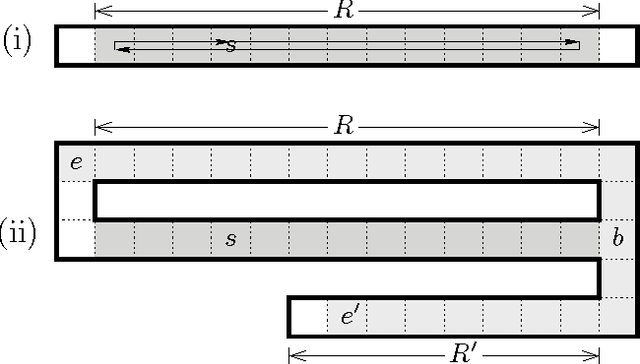
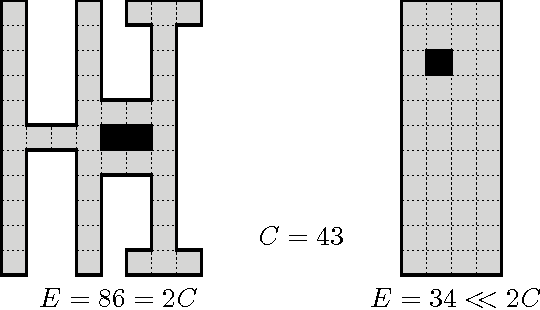
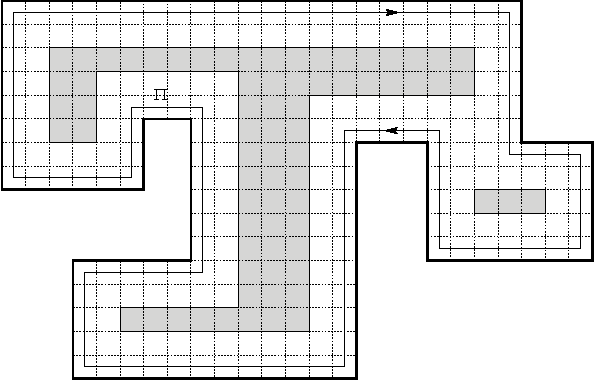
We investigate the exploration problem of a short-sighted mobile robot moving in an unknown cellular room. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 4 adjacent cells exist and which are boundary edges. The robot starts from a specified cell adjacent to the room's outer wall; it visits each cell, and returns to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For abitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/2 E - 3, and for environments containing obstacles we provide a strategy, that is bound by S <= C + 1/2 E + 3H + WCW - 2, where C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-, and H is the number of obstacles, and WCW is a measure for the sinuosity of the given environment.